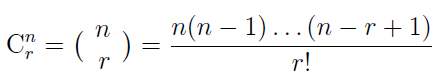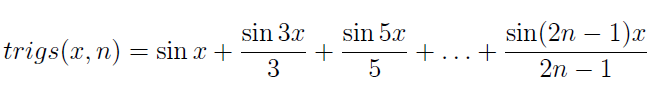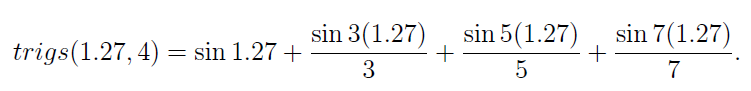MATLAB

Why might you wish to define and construct your own functions and store them in function M-files?

• the mathematical formulation of a function might be quite long and complicated. It might be better to define it separately rather than inside a script M-file.
• the same expression of one or more variables might be required a number of times, either within a single M-file or on different occasions. It is more economical to define the expression as a function in an M-file.
• many MATLAB commands operate on functions which must be held in function Mfiles (see Section 6).

Once a function has been constructed by you in an M-file, it can be used in the same ways as all other MATLAB functions. It can be evaluated, used in any other M-file, or differentiated/integrated in the Symbolic Math Toolbox (see Section 8). In fact, your function can later be used in constructing yet another new function.

The first time MATLAB executes a function M-file, it opens the file and compiles the commands into an internal representation in memory that speeds their execution for all ensuing function calls.

Suppose you wish to construct a function myfunc. Function M-files must follow specific rules.

1. The function name and the M-file name must be identical. Therefore, a function myfunc must be stored in a file named myfunc.m.
2. The first executable statement must be of the form function
        output_variables = myfunc(input_variables)
3. Do not include any clear commands inside a function M-file.
4. Each executable command most probably will finish with a semicolon to avoid printing out numbers each time the function is accessed. Any required values can be printed in the Command Window or in the calling script M-file.
5. Each output variable should be given a value within the M-file.
6. Function M-files terminate execution and return output values when they reach the end of the M-file, or if they encounter the command return beforehand.

Note: You cannot run a function M-file by entering the name of the M-file after the >> prompt as you do with a script M-file. You must give values for the input variables and evaluate as an arithmetic expression.

Example 1: The number of different combinations of r items from n items is given by the binomial coefficient

where n ≥ 1 and r ≥ 0 are integers, r ≤ n. Create a function M-file comb.m containing the function comb(n,r):

function y=comb(n,r)

if r = = 0          % no space between the two equal signs
    y=1;
    return

end

top=prod([n:-1:n-r+1]);

bottom=prod([1:r]);

y=top/bottom;

Now enter after the prompt

comb(4,0) , comb(3,3) , comb(5,2) , comb(9,5) , comb(25,14)

Example 2: Consider the function

where x is the point (or array of points) where the function is being evaluated and n is the number of terms used in this series of sine functions. For example,

Construct the function M-file trigs.m:

function y=trigs(x,n)

% commence the sum for y with the first term

y=sin(x); % y is an array if x is an array

for k=2:n

kodd=2*k-1;

y=y+sin(kodd*x)/kodd;

end

Now evaluate trigs(1.27, 4) (=0.8347) and trigs(1.27, 40) (=0.7822).

You can, of course, now plot a graph of trigs(x, n) for a given n. Construct the following script M-file and then run it.

clear all

x=linspace(-2*pi,2*pi,801);

y=trigs(x,4);

axis([-2*pi 2*pi -1 1])

hold on

plot(x,y)

hold off

Change the trigs(x,4) to each of trigs(x,40) and trigs(x,200) and execute. The graphs you see are part of Fourier Series theory.