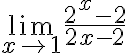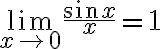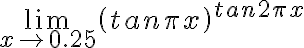MATLAB

Suppose you need to find the limit ie,

$\lim_{x\to1} \frac{2^{x}-2}{2x-2}$

for which both the numerator and denominator tend to zero. This is an example of an indeterminate form of which many others will be investigated in later mathematics using L’Hôpital’s Rule. One method is to find the limit graphically. Enter:

clear all

syms x

f=(2^x-2)/(2*x-2);

ezplot(f,0.95,1.05)

zoom on

You might notice a small hole in the graph at 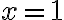$x = 1$ because the expression is undefined there. However, by zooming in, you see that the function is tending towards a value 0.6931 as x → 1. Do you recognise this value? To obtain an exact answer, use the “Maple”s limit command. Add to the above M-file the extra command lim=limit(f,x,1) to obtain the answer lim = log(2) (which is ln 2).

Exercise 1: Change the previous M-file to demonstrate that

$\lim_{x\to0} \frac{ \sin x}{x} = 1$

both graphically and using limit.

Exercise 2: Change the previous M-file to find

$\lim_{x\to0.25}\left(tan \pi x\right)^{tan 2 \pi x}$

(clearly undefined at x = 0.25)

to obtain 0.3679 graphically and 1/e using limit.