Practical 1.2 Buoyancy
| Site: | learnonline |
| Course: | Introduction to Water Engineering |
| Book: | Practical 1.2 Buoyancy |
| Printed by: | Guest user |
| Date: | Wednesday, 7 January 2026, 2:24 PM |
Description
Practical 1.2 Buoyancy
Introduction

A job that may be asked of an engineer is to determine whether or not a body, such as a pontoon or a barge, will be stable as a floating body. Determining the metacentre and the metacentric height of the object is the key to answering this type of question.
The aim of this experiment is to measure the Metacentric Height, GM, of each of two floating vessels using the 'field’ technique. Then you will need to compare this with the theoretical value for GM obtained using the formula.
In this experiment we will use special equipment for measuring metacentric height.
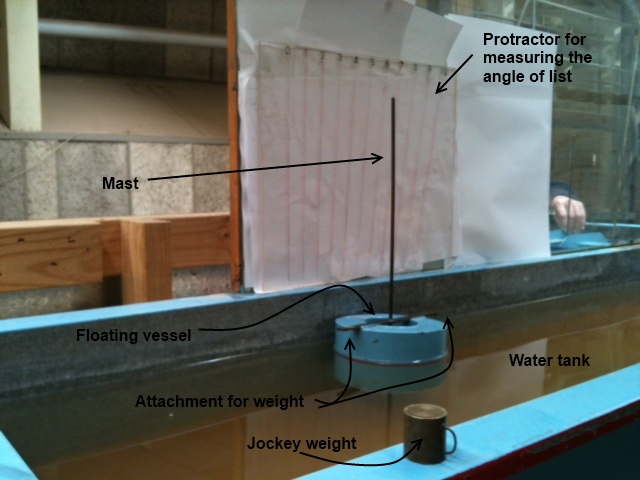
The top image shows the tank for the equipment in situ, in the Water Engineering laboratory.
The lower image is a closer view of one of the floatation devices used in this experiment.
Apparatus
This experiment involves simple apparatus:
- Two floating vessels (one is a buoy made of a cylinder and a cone; the other is a twin-hulled vessel resembling a catamaran). Each vessel has a mast that is used to measure the angle of list, and an attachment on the side to hang the jockey weight
- A small jockey weight for each vessel
- A tank filled with water deep enough to allow the vessels to float
- A large protractor mounted behind the tank to allow visual measurement of the angle of list from the mast
Experimental Method
Watch the video above to see the experiment performed.
For the double hull vessel and the buoy, identify the water plane shape (indicated by the red line) and determine the submerged volume (V).
With the unloaded vessel afloat and steady, measure the residual (angular) deviation of the central mast. Apply a small weight wj at distance dx along the horizontal arm to produce an (angular) deviation of the central mast of less than 8°. Measure the arm distance to the centre of weight wj and determine the angle of list (i.e. deviation with load wj less residual deviation).
Data for Analysis
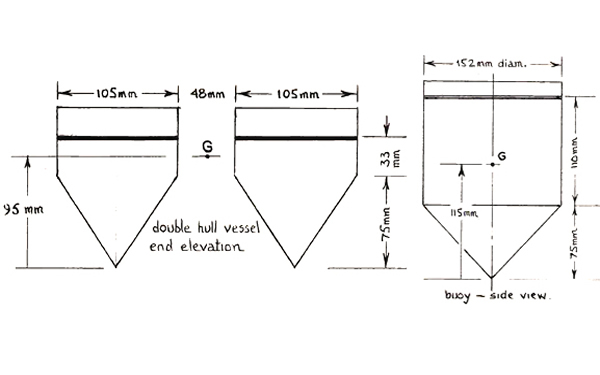
The technical drawings for the floating vessels used in this experiment are provided above. Note that for the double-hull vessel the length ("into the page") is 300mm.
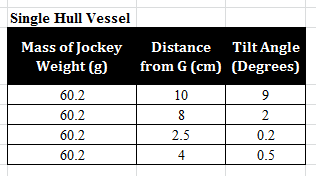
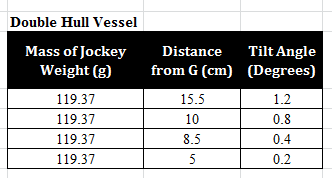
The angle of list data from the experiments are recorded in the tables.
Note: The centre of gravity of a cone or pyramid if height 'h' is located h/4 above the base.
Calculations
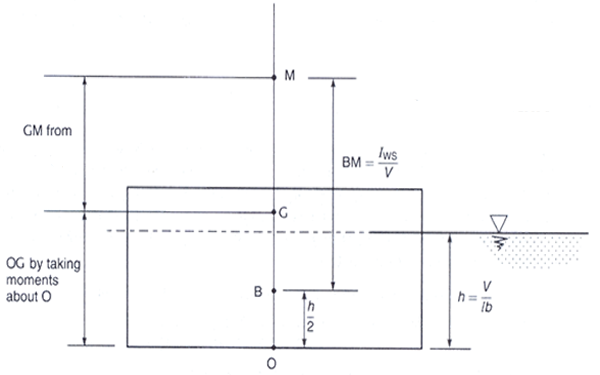
In order to use the appropriate formulae, the following quantities must be known:
Iws : the second moment of area of the water plane shape about the axis of least stability;
V : the submerged volume;
GB : the distance between G, the centre of gravity of the entire vessel, and B, the centre of the submerged volume V
Metacentric Height, GM = Iws/V. ± GB
IMPORTANT: SHOW ALL CALCULATION STEPS
TASK 1: Determine the Metacentric Height of each vessel using the field technique.
TASK 2: Determine the Metacentric Height of each vessel using the formula
TASK 3: Comment on discrepancies between the results given by the two methods for finding Metacentric Height.
Supporting Information
The ‘field’ technique employs a buoyancy expression which is valid for small angles of list:
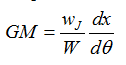
Where wj is the jockey weight
W is the submerged weight
dx is the distance from the centre
θ is the stable angle (radians)