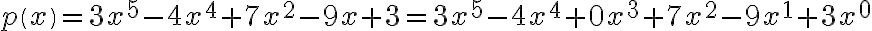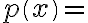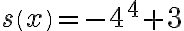Print bookPrint book

Practical 6: Polynomial Functions

Site: learnonline
Course: MATLAB
Book: Practical 6: Polynomial Functions
Printed by: Guest user
Date: Saturday, 23 November 2024, 4:01 PM

Description

MATLAB Short Course

Table of contents

Practical 6

Polynomial Functions

Note: This is a short Practical, but Practical 7 is much longer.

  1. Use coefficient arrays for representing polynomials in MATLAB.
  2. Be able to add and subtract polynomials.
  3. Have a general understanding of the polynomial commands available in MATLAB and be able to apply them.

Working through this Practical

  • The exercises are indented and on separate pages with shaded areas. Do these!
  • Ask your MATLAB eTutor if you have any questions or need advice using the Practical's Forum
  • MATLAB code will always be denoted by the Courier font.
  • An arrow > at the start of the line in an exercise indicates an activity for you to complete.
  • Use the arrows on the top right and bottom right of this display to move between pages, or select a page using the left hand navigation pane.
  • You can also print this resource as a single document (using the print icon in 1.9 or the Admin section in 2.5/2.6).

Please submit your responses to the activities within this practical for formative feedback from your MATLAB eTutor. This word document template can be used to prepare your responses for submission.

Polynomials in MATLAB

In MATLAB, a polynomial is represented by an array of its coefficients of the powers. The MATLAB polynomial functions allow us to perform some useful commands such as addition, multiplication and finding the roots of polynomials.

Example:

p\left(x\right)=3x^{5}-4x^{4}+7x^{2}-9x+3=3x^{5}-4x^{4}+0x^{3}+7x^{2}-9x^{1}+3x^{0}

would be entered as

p = [3 -4 0 7 -9 3],

so that p(1)=3 is a coefficient for 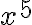x^{5} (term with the highest power), p(2) =-4 is 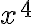x^{4},.., p(6)=3 – for (the lowest power term).

> Exercise: Creating Coefficient Arrays

Write the polynomial p(x) corresponding to array of coefficients q

q = [4 5 -6]                            p\left(x\right) =

> Type in the coefficient array s corresponding to polynomial s(x)

s\left(x\right)=-4^{4}+3                             s=[ ]

Adding and Subtracting

The coefficient arrays of the polynomials can be added and subtracted.

> Exercise: Adding Polynomials with Coefficient Arrays

> Add the following polynomial coefficient arrays:

p = [3 -4 0 7 -9 3]

q = [4 5 -6]

p + q

> What is the problem here? Re-define q as follows and check whether the addition works as you would expect.

q = [0 0 0 4 5 -6]    %Now terms with corresponding powers will be added

p + q
wink Note: To add or subtract two polynomials one should adjust their coefficient arrays putting zeros for absent powers, so that coefficients of terms with the same power will be on the same positions within both coefficient arrays.

 

Commands

Table of some MATLAB polynomial commands

roots([c1 c2 c3]) finds the roots of a polynomial given its array of coefficients, [c1 c2 c3].
poly([r1 r2]) constructs a coefficient array, given the roots, [r1 r2], of the desired polynomial.
polyval(p,x) finds the value of the polynomial with coefficient array p at any given number x.
conv(p,q) multiply two polynomials, and , with coefficient arrays, p and q
[Q,R]=deconv(p,q)

finds the quotient and remainder of polynomial division, p(x)/q(x)

 

> Exercise: Multiplying Polynomials

> Define two polynomials p(x) and q(x) as coefficient arrays p and q in MATLAB

p=[ 1 2 3], q=[2 1]

> use conv function to multiply them

conv(p,q)

> Now, by hand, convert the arrays p and q back to polynomials and multiply them.  Compare your result with the one you received from MATLAB. Is the MATLAB result trustworthy?

> Exercise: Finding Polynomial Roots

> Find the roots of two polynomials, p(x) and q(x), with coefficient arrays p and q

p = [3 -4 0 7 -9 3]

q = [4 5 -6]

> Exercise: Dividing Polynomials

> Multiply p(x) and q(x) by using the conv function and corresponding coefficient arrays.

> Use deconv function to find the remainder and quotient of p(x)/q(x)

 

> Exercise: Re-creating Polynomials from Given Roots

> Find a polynomial with roots r1=5, r2=-5, r3=4, r4=-4.

Plotting

Plotting polynomials with MATLAB can be done using arrays and function m-files.

> Exercise: A Polynomial Plot Function

> Create a function M-file called plotPoly.m that uses an array of polynomial  coefficients to plot the polynomial over an interval specified by the user.

% Input: coefficient array, endpoints array.

% Output: polynomial graph.

% **create x array using linspace**

% **create y array using polyval**

% **plot the graph using the plot command**

> Test your function for p and q from the previous exercise at the interval [-5, 5].

> Exercise: Fitting a Polynomial Curve

> Check the help files under polynomial functions for an appropriate function that fits a polynomial to a set of given data points.

> Create a script M-file called fitPoly.m with the following two cells

1) Fit the points (1,7), (2,-1) and (3,3).

2) Plot the resulting polynomial with your plotting M-file.

Questions?

You may also wish to discuss these questions within the Practical 6 forum, also embedded below. If you think you know the answer, you are welcome to respond.

 

Submit

Please submit your response to Practical 6 for feedback (also embedded below). Use this word document as a template.