Practical 7: Symbolic Toolbox
| Site: | learnonline |
| Course: | MATLAB |
| Book: | Practical 7: Symbolic Toolbox |
| Printed by: | Guest user |
| Date: | Wednesday, 11 February 2026, 1:19 PM |
Description
MATLAB Short Course
Practical 7
Symbolic Toolbox
|
Working through this Practical
- The exercises are indented and on separate pages with shaded areas. Do these!
- Ask your MATLAB eTutor if you have any questions or need advice using the Practical's Forum
- MATLAB code will always be denoted by the Courier font.
- An arrow > at the start of the line in an exercise indicates an activity for you to complete.
- Use the arrows on the top right and bottom right of this display to move between pages, or select a page using the left hand navigation pane.
- You can also print this resource as a single document (using the print icon in 1.9 or the Admin section in 2.5/2.6).
Please submit your responses to the activities within this practical for formative feedback from your MATLAB eTutor. This word document template can be used to prepare your responses for submission.
The Symbolic Toolbox
The past practicals have introduced MATLAB as a powerful programmable graphics calculator. Now we will start showing you how, using MATLAB Symbolic Toolbox, you can, not only solve equations, but also perform algebraic manipulations, such as differential and integral calculus like finding the derivative 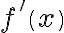 analytically.
analytically.
|
> Exercise: Introducing the Symbolic Toolbox > Type in the following commands. clear all sin(x) >What error message is displayed? |
| The reason for this error message is that you have not first given x a value. However, if we make x a symbolic variable by using the syms x command, then we will be able to create and manipulate formulae without giving x a value first. |
|
> Type in the following and see if you still get the same error message. syms x sin(x) |
|
The syms command is actually a shortcut for the sym command. The longer way of writing is: sym(‘x’) |
|
> Exercise: Symbolic Variables > Type in the following and decide which variables are symbolic. syms x y = x + 1.4*sqrt(x+3) + 5.49 pretty(y) >What does the pretty command do here? |
Solving Equations
The Symbolic Toolbox can be used to find solutions for single or simultaneous equations using the solve command.
Solving a Single Equation
The first task is to solve a single equation 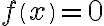 for the variable
for the variable 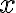 , with the result stored in the variable a. This can be done with command solve.
, with the result stored in the variable a. This can be done with command solve.
a = solve(f,x)
Example
Solving Simultaneous Equations
The solve command not only allows us to find solutions of single equations, but also simultaneous equations.
The command for solving more than one equation is of the form
[a1,a2,...,an] = solve(f1,f2,...,fn,v1,v2,...,vn)
This command can solve 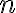 equations for
equations for 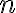 unknowns.
unknowns.
|
> Exercise: Using solve for Simultaneous Equations > Use MATLAB to find the solution of the following simultaneous equations: > This time you will need to create two functions, f1 and f2 to solve f1=0 and f2=0 using the following command: [x,y] = solve(f1,f2) |
Graphing ezplot
The Symbolic Toolbox command ezplot is very convenient for plotting. You will need to specify the symbolic function and the endpoints (optional). By default, the endpoints are 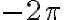 and
and 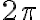 . Hence, you will need to determine endpoints only if they are different from the default ones.
. Hence, you will need to determine endpoints only if they are different from the default ones.
Note: It is possible to plot several functions on the same graph using ezplot and hold on, hold off commands. But the graphs will have the same line properties (colour, thickness, etc) and thus sometimes are hard to distinguish.
|
> Exercise: Using the ezplot command > Type the following code and examine output plots. syms x ezplot(sin(x)) ezplot(sin(x),[-pi pi]) hold on ezplot(sin(x)) ezplot(3*x+2) hold off
|
Plotting Functions
Table for Comparison of 3 Graph Plotting Functions
| Command | plot | fplot | ezplot |
| Required inputs |
|
|
|
| Advantages |
does not need a function formula
full control of graph parameters
|
|
|
| Disadvantages |
|
|
|
| Week | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Grade | 88 | 97 | 100 | 49 | 76 | 33 | 100 | 88 | 87 | 63 | 10 | 82 |
Evaluating Equations
You can find the value of an equation at a point using commands subs, eval.
Algebraic Transformation
The Symbolic Toolbox allows algebraic transformation of a function using the subs command
Numbers
Let’s use the following example to illustrate the difference between symbolic and standard numbers representation.
Number Format
By default, the Symbolic Toolbox uses integers or rational fractions such as 1, 1/2.
Otherwise, it uses a real number approximation by a fraction of large integers, eg 3333/100000. Command sym(number) converts a number to its symbolic form while double(number) command reverses symbolic representation to MATLAB standard format. Therefore, sym command means ‘switch to Symbolic Toolbox’, while double means ‘switch back to MATLAB’
|
> Exercise: Understanding Numerical Formats > For the following numbers, find out their symbolic and standard formats. |
||
| Number | Symbolic Command | Standard Command |
| 11/13 | sym 11/13 | double (11/13) |
| 3.85 | ||
| pi | ||
| 0.33333 | ||
| (4/5)2 | sym((4/5)^2 | double ((4/5)^2) |
| 591/2 | ||
| e1 | ||
| sin(1) | ||
Algebraic Operations
A table of the most common Symbolic Toolbox Algebraic Operations
Differentiation and Integration
The Symbolic Toolbox features special commands for differentiation and integration. This practical will focus only on the basic diff and int commands. The default variable for integration or differentiation is 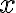 (first), or
(first), or 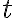 (if there is no
(if there is no 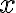 ) but you can specify another symbol.
) but you can specify another symbol.
Numerical Integration
Sometimes there is no explicit expression because the antiderivative can’t be written in terms of familiar functions. Instead MATLAB can use numerical techniques to find the definite integral by using the double command.
|
> Exercise: Limitations of Integration Techniques > Use the int command to find the indefinite integral, and observe the output. intf = int(f,v) > Modify the above command to find the definite integral between v=0 and v=pi. Does the command work? > Observe what happens if you use the double command. defint=double(int(f,v,0,pi)) |
Toolbox Functions
Questions?
You may also wish to discuss these questions within the Practical 7 forum, also embedded below. If you think you know the answer, you are welcome to respond.
Submit
Please submit your response to Practical 7 for feedback (also embedded below). Use this word document as a template.
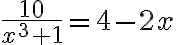
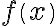
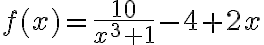
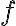
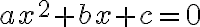
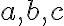
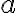
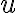
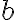
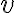
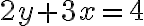
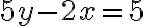
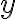
 Note: If you plot several functions using
Note: If you plot several functions using 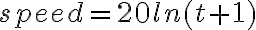
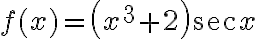
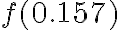
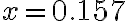
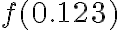
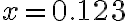
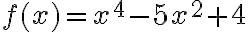
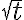
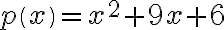
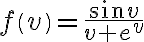
![[a,b] [a,b]](https://lo.unisa.edu.au/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif)