3. Probability models used for discrete variables
Example: Consider an experiment in which three (3) white blood cells are tested for lymphocytes. Let L denote a lymphocyte and N denotes a normal cell. Let the probability that a cell is a lymphocyte be 2/3. Then the sample space and corresponding probabilities are:
L L L (2/3)3
L L N (2/3)2 (1/3)
L N L (2/3)2 (1/3)
N L L (2/3)2 (1/3)
L N N (1/3)2 (2/3)
N L N (1/3)2 (2/3)
N N L (1/3)2 (2/3)
N N N (1/3)3
Let the variable X be the number of lymphocytes in the three white blood cells. What is the probability distribution of X?
|
Values of X |
Outcomes |
Probabilities |
|
X = 0 X = 1 X = 2 X = 3 |
N N N L N N or N N L or N L N L L N or L N L or N L L L L L |
P(X = 0) = (1/3)3 = 0.03704 P(X = 1) = 3 (1/3)2 (2/3) = 0.22222 P(X = 2) = 3 (2/3)2 (1/3) = 0.44444 P(X = 3) = (2/3)3 = 0.29630 |
|
|
|
The expected value (average value) of a discrete random variable is defined as:
Examples:
- The gambling experiment above, the expected gain is:
m = (3) (0.125) + (1) (0.375) + (-1) (0.375) + (-3) (0.125) = 0.
- The white blood cells experiment, the expected number of white cells is:
m = (0) (0.03704) + (1) (0.22222) + (2) (0.44444) + (3) (0.29630) = 2.
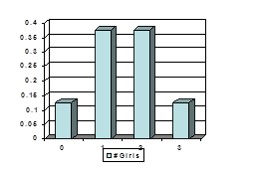
- The Number of girls in a family with three children:
|
Value x |
P(X=x) |
|
0 1 2 3 |
0.125 0.375 0.375 0.125 |
m = (0) (0.125) + (1) (0.375) + (2) (0.375) + (3) (0.125) = 1.5.