Definition: An experiment which can result in only one of two mutually exclusive outcomes (e.g., male/female, dead/alive, diseased/non-diseased,…) is called a “Bernouilli Trial”. One of the outcome is denoted “success” and the other “failure”; probability of success is known, let’s say, p (e.g., p = 0.5; 0.25); probability of failure is 1-p. This probability distribution is usually denoted by Be(p).

Consider n independent trials from an experiment with only two possible outcomes, at each trial, which are denoted as “success” and “Failure”. Furthermore, the probability of a success is the same at each trial, denoted p, and hence the probability of a failure at each trial is 1-p. Let the variable X be the number of successes in n trials. Then, the probability distribution of X is known as the Binomial distribution.

1. Example of the number of girls in a family with three children: n = 3; p = 0.5, as seen above; Mean = (3) (0.5) = 1.5; variance = (3) (0.5) (0.5) = 0.75 (= 3/4).

2. Example of white blood cells:  n = 3; p = 2/3; Mean: = (3) (2/3) = 2; variance: = (3) (2/3) (1/3) = 2/3.

3. Example of recovery from delicate surgery: n = 20; p = 1/4 = 0.25; X ~ Bin(20, 0.25);

(a) P(X < 3) = P(X = 0 or X = 1 or X = 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.09126

(b) P(X > 5) = 1- P(X  5) = 1- P(X = 0 or X = 1 or X = 2 or X = 3 or X = 4 or X = 5) =

 1- (P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)) = 0.38283

Note: There exists as well a freeware program, StaTable developed by Cytel Software Corporation, that computes probabilities for various probability distributions. (https://lo.unisa.edu.au/pluginfile.php/986155/mod_folder/content/0/setup.exe?forcedownload=1).

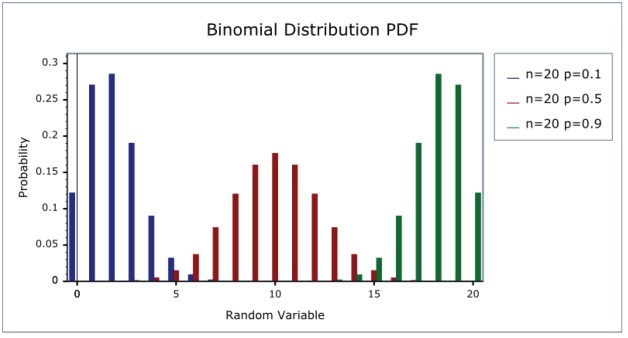
Some examples of Binomial probability distributions:

Keep the success fraction p fixed at 0.5, and vary the sample size (n)

Alternatively, we can keep the sample size fixed at n = 20 and vary the success fraction p: