5. Poisson distribution
Examples
The Poisson distribution is applicable for discrete variables counting the number of events occurring in a certain interval of time (number of emergency calls over a day, a week, a year,…, etc.) or unit of measurement such surface area (number of bacterial colonies on agar plate, number of deaths in a given unit of intensive health care,…., etc.) or volume (number of E. coli bacterial colonies in 1 mL of water sample).
Assumptions underlying the Poisson distribution
- The probability of observing the event of interest is directly proportional to the length of that interval (interval of time, or surface area, or volume,….,etc.);
- The number of events occurring per unit of time or surface area or volume is the same throughout the entire interval;
- If an event occurs within one subinterval, it has no bearing on the probability of an event in the next subinterval and the number of events reported in any two distinct intervals are independent random variables.
Examples
(1) Consider the distribution of the number of deaths attributed to typhoid fever over a period of time, say 1 year (Infectious Disease).
(2) Consider the distribution of the number of bacterial colonies growing on an agar plate (Bacteriology).
Example 1 Infectious disease:
Suppose that the number of deaths attributable to typhoid fever over 1-year period is Poisson with parameter m = 4.6 (that is, there are, on average, 4.6 deaths per year attributable to typhoid fever). What is the probability of getting (a) no deaths, (b) at least 1 death, over a 6-month period?
Example 2 Breast Cancer:
Suppose that we are interested in the genetics susceptibility to breast cancer. We find that 4 out of 1000 women aged 40-49 whose mothers have had breast cancer develop breast cancer over the next year of life. We would expect from large population studies that 1 in 1000 women of this age group will develop a new case of the disease over this period of time. How unusual is this event?
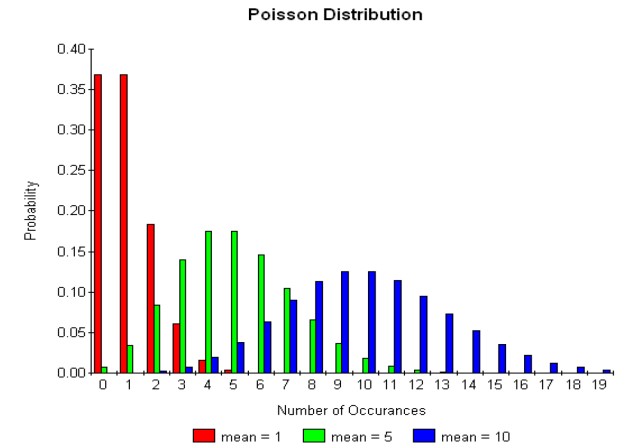
Visual examples of Poisson distributions