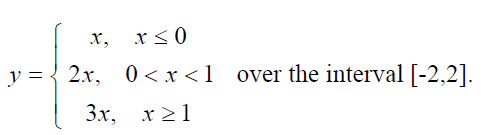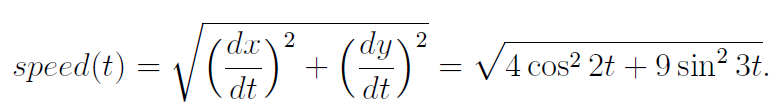In this section we will use MATLAB ’s plot command to produce graphs. In Sections 6 and 8 you will see there are two other commands to create graphs, namely fplot which uses function M-files and ezplot which is inside the Symbolic Math Toolbox.

If x = {x(1), x(2), . . . , x(n )} and y = {y(1), y(2), . . ., y(n)}, then the MATLAB command plot(x,y) opens a graphics window, called a Figure window, scales the axes to fit the data, plots the points (x(1), y(1)), (x(2), y(2)), . . . , (x(n), y(n)), and then graphs the data by connecting the points with straight lines. If a Figure window already exists, another plot command clears the current Figure window by default (unless instructed not to do so) and draws a new plot. Type in the following as an attempt to graph y = sinx for 0 ≤ x ≤ 2π. [You could replace the last two lines with plot(x,sin(x)).]

clear all

x=linspace(0,2*pi,11);

y=sin(x);

plot(x,y)

Clearly this attempt is unacceptable because we have not used sufficient points! Change the 11 to 201 and execute the code again.

In general, most graphs can be satisfactorily plotted using arrays of, say, 101 to 201 points, although erratic or wildly fluctuating functions would require many more points. Please note that you only need two points to plot a single straight line. For example, to plot a straight line from the point (1,7) to the point (3,-5) you need the command plot([1 3],[7 -5]).

Note: Students often get this wrong by forgetting that the first array always contains the x-coordinates, not the two coordinates of the first point. Similarly, the second array contains the y-coordinates.

Exercise 1: Plot the graph of y = xex/x² − π² for −3 ≤ x ≤ 2 using a step-size of 0.02. You will need three dots in the expression to generate the array y.

Exercise 2: Plot the graph of y = sin9x + sin10.5x + sin12x for −π ≤ x ≤ π using 601 points.

Plotting several graphs on the same axes

Example 1: Suppose you want to plot the oscillations y1 = cost, y2 = cos3t and their sum y3 = y1 + y2, for 0 ≤ t ≤ 4π, on the same axes. Here t is measured in seconds and y1, y2, y3 are measured in cm.

clear all

t=linspace(0,4*pi,201);

y1=cos(t); y2=cos(3*t); y3=y1+y2;

plot(t,y1,t,y2,t,y3)

You notice that we found the three y-arrays in a single line of code and they were plotted in different colours. But the empty space at the right end of the graphs is annoying, and how can we label the output so that each graph can be identified? There are many facilities provided by MATLAB to assist you in producing attractive, meaningful graphs. Change the above M-file to the following (this is important!):

clear all

t=linspace(0,4*pi,201);

y1=cos(t); y2=cos(3*t); y3=y1+y2;

axis([0 4*pi -2 2]) % specifies the axes limits

hold on

plot(t,y1,’b--’,t,y2,’g:’,t,y3,’r’)

legend(’y1=cos(t)’,’y2=cos(3*t)’,’y3=y1+y2’)

plot([0 4*pi],[0 0],’k’) % adds the t axis in black

xlabel(’time in seconds’)

ylabel(’displacement in cm’)

title(’oscillations’)

hold off

A short diversion

To get assistance with the MATLAB commands featured above and in the next example, you can use the help facility. Enter each of the following after the >> prompt and carefully read the information until you understand precisely what each of the lines in the previous (or next) M-file is accomplishing.

• help axis
• help plot
• help hold
• help legend
• help text
• help print a menu of print options for your Figure

Alternatively, if you do not know the precise name of a MATLAB command for which you need help, you can click on the Help button at the top of the MATAB Command Window, then click on “MATLAB Help” followed by “MATLAB Functions Listed by Category” and then on a topic of interest. For example, to get help on many graphics related commands, click on Plotting and Data Visualization.

Another help option is the lookfor facility. Suppose you were interested in commands involving the use of complex numbers. After the >> prompt enter lookfor complex.

Example 2: By using hold on and hold off, you can plot several functions on the same axes using a number of plot commands. The functions f(x) = x2 and f−1(x) = √x are inverse functions for x ≥ 0 and hence their graphs must be reflections through the line y = x. Execute the following M-file, carefully noting the results of each command:

clear all % file available in M-files folder as file1.m

axis([0 4 0 4]), axis square

hold on

x1=linspace(0,2,101);

y1=x1.^2; % note the dot

plot(x1,y1)

x2=linspace(0,4,101);

y2=sqrt(x2);

plot(x2,y2)

plot([0 4],[0 4],’k:’) % dotted line in black from (0,0) to (4,4)

text(1.5,3.5,’y=x^2’)

text(3.1,1.7,’y=sqrt(x)’)

grid on % adds grid lines if you want them

title(’reflection property of inverse functions’)

Zoom on

MATLAB provides an interactive tool to expand sections of a plot to see more detail. This is particularly useful if you need to obtain accurate information about where two graphs intersect, or to find the coordinates of an extreme point. The command zoom on, either in your M-file or after the >> prompt turns on the zoom mode. Then go to the Figure window, place the pointer where you want an enlargement and click with the left button. Continue this process and you can zoom in to obtain three or four decimal place accuracy.

Example: Suppose you want to find graphically the point of intersection of y = tanx and y = 1− x3. (Note that there are other non-graphical ways of doing this, described in Sections 6 and 8.) Firstly, plot both of these functions on the same axes for −1.2 ≤ x ≤ 1.2, with at least 800 points to enable zooming. You might also like to add the x and y axes to obtain a figure similar to that on the previous page. Enter the command zoom on. Then zoom in at the point of intersection until you are able to find its coordinates to the accuracy of (0.6376 , 0.7408).

Exercise: Plot y = 10e−t sin t for 0 ≤ t ≤ 2π and then use zoom on to find its maximum value.

Creating separate graphs in one M-file

If you want two separate Figures to be created in one M-file, you can use the figure(n) command where n is a number associated with the window and precedes the set of plotting

commands.

Example: At time t seconds, t ≥ 0, a moving point has coordinates x = sin2t, y = cos3t (metres), and so its speed is given by

Plot the path taken by the point over one cycle 0 ≤ t ≤ 2π, where t is regarded as a parameter, and also plot the speed against time. Use the following M-file. (You can add your own labels, etc.)

clear all % file available in M-files folder as file2.m

t=linspace(0,2*pi,500);

x=sin(2*t);

y=cos(3*t);

figure(1)

plot(x,y)

axis equal % same scale (metres) on each axis

speed=sqrt(4*cos(2*t).^2+9*sin(3*t).^2); % note the dots

figure(2)

axis([0 2*pi 0 4])

hold on

plot(t,speed)

hold off