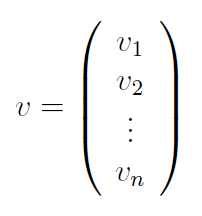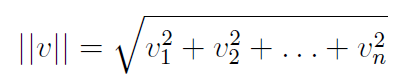Each array that was discussed in Section 4 was, in effect, a row vector or row matrix. But you are aware that a rectangular array represents a matrix and a single array column represents a column vector.

To construct a matrix with m rows and n columns (called an “m by n matrix”, written m×n matrix), each row in the array ends with a semicolon. For example, run the following M-file mat.m:

A=[3 -5 1;-2 0 -4;6 7 9]

B=rand(3,3)

C=[1 -3;-1 5;2 8]

The element A(i,j) is in the i^th row and j^th column. Hence, after the prompt, enter

a23=A(2,3), b31=B(3,1), c12=C(1,2)

The comma separates the row number(s) from the column number(s).

What is A(3,[2 3]), B([1:2:3],[1:2:3])?

A single colon “:” before the comma means “take all rows”, whereas a single colon after the comma means “take all columns”. Hence A(:,2) is column number 2 in the matrix A while is the first row of B.

Providing matrices have the same shape they can be added or subtracted. Providing they have compatible shapes they can be multiplied using the established rules for matrix multiplication. Hence calculate after the prompt D=2*A-B, F=A*B, G=A*C, Asq=A^2. However, B+C and C*A produce error messages.

Note: A.^2 does not square the matrix but squares each element in the matrix. Similarly, A.*B is not matrix multiplication but merely multiplies the corresponding positions in the two matrices.

det(A) is the determinant of A, written |A|.

A' is the transpose of A and is written in mathematics as A^T. It is formed by interchanging the rows and columns. Hence, if you need to input the column vector

you could enter v=[v1;v2;...;vn] or v=[v1 v2 ...vn]'.

The magnitude or Euclidean norm of the vector v, given by

is represented in MATLAB  by norm(v).

If A is a square matrix with |A| = 0, then inv(A) represents the inverse of A, denoted in mathematics by A⁻¹.

The n × n identity matrix I is represented in MATLAB by eye(n). For the matrix A at the beginning of this section, verify that A*inv(A)=inv(A)*A=eye(3).