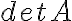Exercise 1: Suppose you want to find the two zeros of the quadratic ax2 + bx + c. (As you would expect, Matlab already has a procedure to do this automatically, but let us solve this independently.) Firstly, to solve 5x2 −17x−12 = 0, you should create, save and execute an M-file quadzeros.m (for example)

clear all

a=5, b=-17, c=-12

x1=(-b+sqrt(b^2-4*a*c))/(2*a)

x2=(-b-sqrt(b^2-4*a*c))/(2*a)

Then change this to find the zeros of each of the quadratics

3x² + 5x − 13       2x² − 7x + 23          2.34x² + πx − √6

Exercise 2: Suppose the three sides of a triangle have lengths (in cm) a = 11.7, b = 6.9, c = 7.1. Find the three angles A,B,C using the cosine rule

a² = b² + c² − 2bc cosA

and the sine rule

a/sinA = b/sinB = c/sinC

Convert the angles into degrees.

Construct the following in an M-file triangle.m, and then execute it.

clear all

a=11.7; b=6.9; c=7.1;

% let cA represent cos(A), and sB represent sin(B)

cA=(b^2+c^2-a^2)/(2*b*c);

A=acos(cA);

sB=b*sin(A)/a;

B=asin(sB);

C=pi-A-B;

% convert angles into degrees for output

A=A*180/pi; B=B*180/pi; C=C*180/pi;

fprintf(’angle A is %6.2f degrees \n’, A)

fprintf(’angle B is %6.2f degrees \n’, B)

fprintf(’angle C is %6.2f degrees \n’, C)

You will notice that the fprintf command produces neat output. In each case, the variable to be printed is at the end, while %6.2f stipulates where the value is to be printed along with how many positions (6) and how many decimal places (2). The \n moves to a new line after printing whatever precedes it, in preparation for more output.

Exercise 3: Consider the two simultaneous linear equations

a₁₁x + a₁₂y = b₁

a₂₁x + a₂₂y = b₂

MATLAB provides various ways to solve this automatically, given values for the coefficients, as we shall see later. But for now, you will write your own M-file. You will need to give values for the four coefficients and the numbers on the right hand side, find $detA$ = a₁₁a₂₂ − a₁₂a₂₁ so that

x = a₂₂b1 − a₁₂b_{2 /} detA and y = a₁₁b₂ − a₂₁b₁ / detA

providing detA ≠ 0. Test your M-file on the following two problems:

2x − 3y = 2              3x − 11y = 17

5x + 6y = 59           −6x + 22y = 23

The solution of the left system is x = 7, y = 4. The right system clearly does not have a solution.

Entering Long Expressions: if an expression does not fit on a single line, use three dots . . . to indicate that the statement continues on the next line. Do not leave any unnecessary blank spaces and press Enter or Return immediately to advance to the next line, and continue entering the statement. Be careful to create this break at a sensible point in the expression, preferably after a comma or mathematical operation.