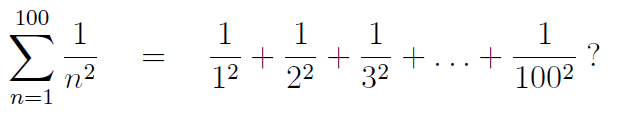4. Arrays
Calculating
Performing arithmetic calculations on arrays containing large data sets is considerably easier with MATLAB than with other computer languages such as C or Pascal. It is precisely the ease of array manipulation that makes MATLAB suitable for mathematical, scientific and engineering applications.
Basic arithmetic operations on arrays
If X is an array and a, b are scalar values, then a∗X+b creates a new array by multiplying all the elements of X by a and then adding b to each position. What do you expect X/a+b to give?
Enter X=[1:8] after the prompt. Then execute
y=10*X+7
z=(y-7)/10 %why is this the same as X?
v=3*X/2 -1
If A,B are two arrays containing the same number of elements and c1, c2 are scalars, then expressions of the form c1A ± c2B will create new arrays. Enter the following:
clear all
A=[1:2:11] , B=[8:-1:3]
C=B-A
D=(3*A-4*B)/2 + 5
However, there are some other very important differences. Later you will see that MATLAB includes standard operations with matrices and vectors, which are also examples of arrays. Hence, to distinguish those operations, a dot must be placed immediately before the ∗ / ^ operators in each of the following circumstances, where A,B are arrays of the same length and c is a scalar.
A .* B A ./ B c ./ A A .^ B c .^ A A .^ c
In other words, a dot is required before the operator whenever two arrays are multiplied together, whenever you divide by an array, and whenever an array occurs in any power expression. These always create a new array of the same length as A (and B). Enter the following and take careful note of the answers:
clear all
X=[1 2 3 4] , Y=[-1 4 2 1/2]
K1=X.*Y % multiply the corresponding elements
K2=X./Y % divide the corresponding elements
K3=5./Y % divide 5 by each element of Y
K4=X.^Y % raise the numbers in X to the corresponding power in Y
K5=2.^X % raise 2 to the power of each number in X
K6=Y.^3 % cube each element in Y
Example 1: Create an array curo that contains the cube roots of all integers from 24 to 30.
clear all
A=[24:30];
curo=A.^(1/3) % note the dot and brackets
Rather than introducing the array A at all, this could be done immediately using
clear all
curo=[24:30].^(1/3)
Example 2: What is the value of the sum
Enter the following:
clear all
% create an array n
n=[1:100]; % note the semi-colon (do not print out the 100 values)
b=1./n.^2; % note the two dots (and the semi-colon)
total = sum(b) % you should get total = 1.6350
Or you could be clever and find this total without actually introducing the array names n, b.
clear total
total = sum([1:100].^(-2)) % note the dot as [1:100] is an array
Exercise: Consider the 40 values n7/2n for n = 1, 2, 3, . . . , 40. Use MATLAB ’s max function to determine the largest of these values and the number n for which it occurs. You should obtain that it is the 10th value equal to 9.7656e+003 which you must know is scientific notation for 9765.6.
Using mathematical functions on arrays
Given an array X and a function f, then the MATLAB command Y=f(X) produces a new array Y such that the elements of Y are Y (i) = f(X(i)) (or in mathematics Yi = f(Xi)). This, coupled with the basic arithmetic operations on arrays discussed earlier enables powerful but simple data manipulation.
Example 1: Enter the following into an M-file and then execute it.
clear all
X=[0:pi/6:2*pi]
Y=sin(X)
Z1=1-2*Y.^2 % note the dot
Z2=cos(2*X) % why are Z1 & Z2 equal?
Example 2: Consider the values tan2(m) for m = 1, 2, . . . , 200. How many of these values are greater than 100?
clear all
m=[1:200];
b=tan(m).^2; % note the dot
c=find(b>100) % finds the positions, not the actual values
number=length(c) % answer is 13 values
Example 3: You should know the classic limit lim x→0 sin x/x = 1. Demonstrate this by evaluating sin x/x for each of x = 0.1, 0.01, . . . , 0.00000001.
clear all
format long % use 16 characters for each value
x=0.1.^[1:8] % note the dot because [1:8] is an array
y=sin(x)./x % note the dot because x is an array
Exercise: The output from an engineering system is y = t2e−t sin t for t ≥ 0. We want to find the maximum value which certainly occurs within 0 ≤ t ≤ 3. Although MATLAB has other more efficient ways of doing this (see later), you could merely investigate this function by dividing the interval [0,3] into 10,000 subintervals (10,001 points). Fill in the missing code in the second and third lines in the following M-file, recalling that the exponential function ex is exp(x) in MATLAB . You should obtain ymax=0.5239, posn=5759, time=1.7274.
clear all
t=linspace( , , );
y= ;
[ymax,posn]=max(y) % use array max function
time=t(posn) % finds corresponding value in the t array