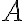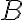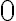The density matrix

$\rho_{AB} = \frac{1}{2}|0\rangle\langle0|_A\otimes|1\rangle\langle1|_B + \frac{1}{2}|+\rangle\langle+|_A\otimes|-\rangle\langle-|_B$

is separable because it takes the form of Eq. (1).

Subsystems $A$ and $B$ are not entangled, but they are (classically) correlated.

The state $|\psi\rangle_{AB} = \frac{1}{\sqrt{2}}(|01\rangle_{AB} + |11\rangle_{AB})$ is separable because

$|\psi\rangle_{AB} = \frac{1}{\sqrt{2}}(|01\rangle_{AB} + |11\rangle_{AB}) = \frac{1}{\sqrt{2}}(|0\rangle_A+|1\rangle_A) \otimes |1\rangle_B = |+\rangle_A\otimes|1\rangle_B.$

The Einstein-Podolsky-Rosen (EPR) pair $|\text{EPR}\rangle_{AB} = \frac{1}{\sqrt{2}}(|00\rangle_{AB} + |11\rangle_{AB})$ is entangled because it cannot be expressed in the form of Eq. (1).

This example is meant to highlight the difference between the following two states:

$\rho_{AB} = \frac{1}{2}|0\rangle\langle0|_A\otimes|0\rangle\langle0|_B + \frac{1}{2}|1\rangle\langle1|_A\otimes|1\rangle\langle1|_B \quad\text{and}\quad \sigma_{AB} = |\text{EPR}\rangle\langle\text{EPR}|_{AB},$

where $|\text{EPR}\rangle_{AB} = \dfrac{1}{\sqrt{2}}(|00\rangle_{AB} + |11\rangle_{AB})$. $\rho_{AB}$ is separable whereas $\sigma_{AB}$ is not.

Consider the outcomes of measuring subsystem $A$ in $\rho_{AB}$ and $\sigma_{AB}$ in the standard basis and in the Hadamard basis.

Measuring subsystem $A$ of $\rho_{AB}$ in the Hadamard basis:

Define the measurement operators to be $\mathbf{M}_{+A}\otimes\mathbf{I}_B$ and $\mathbf{M}_{-A}\otimes\mathbf{I}_B$, where $\mathbf{M}_{+A}=|+\rangle\langle+|_A$ and $\mathbf{M}_{-A}=|-\rangle\langle-|_A$. Clearly, $\mathbf{M}_{+A}^\dagger\mathbf{M}_{-A}=\mathbf{0}$ and $\mathbf{M}_{+A} + \mathbf{M}_{-A} = \mathbf{I}$.

Using projective measurement, the post-measurement state conditioned on measurement outcome $|+\rangle$ is

$\rho'_{AB|+} = \dfrac{(\mathbf{M}_{+A}\otimes\mathbf{I}_B)\rho_{AB}(\mathbf{M}_{+A}\otimes\mathbf{I}_B)}{\text{tr}\{(\mathbf{M}_{+A}\otimes\mathbf{I}_B)\rho_{AB}\}}.$

Let us work out the numerator and the denominator separately, starting with the numerator:

$\begin{split} &(\mathbf{M}_{+A}\otimes\mathbf{I}_B)\left( \dfrac{1}{2}|0\rangle\langle0|_A\otimes|0\rangle\langle0|_B + \dfrac{1}{2}|1\rangle\langle1|_A\otimes|1\rangle\langle1|_B \right)(\mathbf{M}_{+A}\otimes\mathbf{I}_B) \\ &= \dfrac{1}{2}\left\{ |+\rangle\langle+|_A|0\rangle\langle0|_A|+\rangle\langle+|_A\otimes|0\rangle\langle0|_B + |+\rangle\langle+|_A|1\rangle\langle1|_A|+\rangle\langle+|_A\otimes|1\rangle\langle1|_B \right\} \\ &= \dfrac{1}{4}\left\{|+\rangle\langle+|_A\otimes|0\rangle\langle0|_B + |+\rangle\langle+|_A\otimes|1\rangle\langle1|_B \right\}. \end{split}$

The preceding equality follows from these identities, which you will derive in the practical:

$\begin{align} |+\rangle\langle+||0\rangle\langle0||+\rangle\langle+| &= \dfrac{1}{2}|+\rangle\langle+|, \\ |+\rangle\langle+||1\rangle\langle1||+\rangle\langle+| &= \dfrac{1}{2}|+\rangle\langle+|. \end{align}$

The denominator is:

$\begin{split} &\text{tr}\left\{(\mathbf{M}_{+A}\otimes\mathbf{I}_B)\left( \dfrac{1}{2}|0\rangle\langle0|_A\otimes|0\rangle\langle0|_B + \dfrac{1}{2}|1\rangle\langle1|_A\otimes|1\rangle\langle1|_B \right)\right\} \\ &= \text{tr}\left\{\dfrac{1}{2}|+\rangle\langle+|0\rangle\langle0|\otimes|0\rangle\langle0| + \dfrac{1}{2}|+\rangle\langle+|1\rangle\langle1|\otimes|1\rangle\langle1|\right\} = \dfrac{1}{2}. \end{split}$

The preceding computation is tedious but straightforward given the right tool (e.g., NumPy). Combining the results for the numerator and denominator, we get

$\rho'_{AB|+} = \dfrac{1}{2}|+\rangle\langle+|_A\otimes|0\rangle\langle0|_B + \dfrac{1}{2}|+\rangle\langle+|_A\otimes|1\rangle\langle1|_B.$

Thus, upon measuring a $|+\rangle$ on subsystem $A$, subsystem $B$ can be in either $|0\rangle$ or $|1\rangle$ at equal probabilities; we say the reduced state on $B$ is maximally mixed.

Measuring subsystem $A$ of $\sigma_{AB}$ in the Hadamard basis:

The pair of $|00\rangle_{AB}$ and $|11\rangle_{AB}$ can be re-expressed as $|++\rangle_{AB}$ and $|--\rangle_{AB}$, because ‘$+$’ is orthogonal to ‘$-$’ just as ‘$0$’ is orthogonal to ‘$1$’.

The preceding statement implies when $|+\rangle$ is measured on subsystem $A$, subsystem $B$ is in state $|+\rangle$ as well.

Correlations in $\sigma_{AB}$ are thus stronger than those in $\rho_{AB}$.