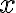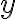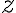Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
A |
|---|
Abstract algebra | |||
|---|---|---|---|
See 👇 attachment or the latest source on Overleaf, on the topics of groups and Galois fields (pending). | |||
Ancilla | ||||||
|---|---|---|---|---|---|---|
An ancilla (system) is an auxiliary quantum-mechanical system [ETS18]. Think of ancilla as something extra that is used to achieve some goal [Pre18]. References
| ||||||
Axiomatic approach to quantum operations | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
In quantum information theory, the foundation of quantum cryptography, the concepts of general/generalised measurements and quantum channels are rooted in the concept of quantum operation [Pre18, Sec. 3.2.4].
While the time evolution of a closed quantum system can be expressed using a single unitary operator, the time evolution of an open quantum system is much less straightforward [HXK20], and this is where the theory of quantum operations come in. Here, the axiomatic approach in [NC10, Sec. 8.2.4] to defining quantum operations is discussed, starting with Definition 1. Definition 1: Quantum operation [NC10, p. 367]
A quantum operation is a map from the set of density operators for the input space to the set of density operators for the output space , that satisfies these axioms:
Justification of Axiom 1: In the absence of measurement, by itself completely describes the quantum operation, and Axiom 1 reduces to the requirement that ; in this case, the quantum operation is trace-preserving.
Justification of Axiom 2: Let , then where is a normalisation factor. By Bayes’ rule, Justification of Axiom 3: A quantum operation maps a density operator to a density operator — by itself or as part of a larger system — and density operators are always positive, so must be a completely positive map. Example 1 [Pre18, p. 19]
This example is meant to show that the transpose operation is not a completely positive map and hence not a quantum operation. We first observe that is positive if is positive because the quadratic form However, the transpose operation is not completely positive due to the following. Suppose system contains entangled subsystems and , and has state , ignoring the normalisation constant. Above, we applied the identity . Now consider the composite map , where is the transpose operation, which transforms to . Applying the composite map to , we get Applying the composite map to the above, we get back Therefore, if we represent the map with a square matrix, the matrix is involutory (square = identity), and it is trivial to show that the eigenvalues of an involutory matrix are (see below), implying the composite map is not positive. In other words, the transpose operation is not a completely positive map, and hence not a quantum operation. Axioms 1-3 lead to the following important theorem. Theorem 1 [NC10, Theorem 8.1]
In Theorem 1,
Example 2 [MM12, p. 176]
The freedom in the operator-sum representation is especially useful for studying quantum error correction. Theorem 2 [NC10, Theorem 8.3]
Watch lectures on Kraus representations by Artur Ekert, inventor of the E91 QKD protocol: References
| ||||||||||||||||||
B |
|---|
BB84: Overview | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Quantum key distribution (QKD) is a method for generating and distributing symmetric cryptographic keys with information-theoretic security based on quantum information theory [ETS18]. A QKD protocol establishes a secret key between two parties — let us call them 👩 Alice and 🧔 Bob as per tradition — connected by 1️⃣ an insecure quantum channel and 2️⃣ an authenticated classical channel [Gra21, Sec. 3.1].
A QKD protocol typically proceeds in two phases [Wol21, Ch. 4]:
The security of QKD hinges on the principles of quantum mechanics, rather than the hardness of any computational problem, and hence does not get threatened by advances in computing technologies.
Theorem 1: No-cloning theorem [WZ82]
It is not possible to perfectly clone an unknown quantum state. The earliest QKD protocol is due to Bennett and Brassad [BB84] and is called BB84, named after the authors and the year it was proposed. QKD leverages physical mechanisms, so unavoidably we need to discuss the physical mechanisms that underlie/enable BB84, which are based primarily on the polarisation of photons [Wol21, Sec. 1.3.1]. PolarisationThe polarisation of photons specifies the geometrical orientation of the oscillation of its electromagnetic field.
We only consider linear polarisation here. For linear polarisation, we distinguish between two bases:
Consider the effect of polarisation filters depicted in Fig. 1:
Thus, measuring a diagonally polarised photon in the rectilinear basis, and similarly measuring a vertically/horizontally polarised photon in the diagonal basis, give a random result.
With knowledge of polarisation in mind, let us now discuss the quantum transmission phase of BB84, which involves encoding of classical bits into quantum states, communication over a quantum channel, and decoding of quantum states into classical bits. Quantum transmission phaseThis phase of the protocol involving 👩 Alice and 🧔 Bob goes like this [Wol21, Sec. 1.3.2]:
An illustration of the process above can be found Fig. 1. Since the polarisation state of each photon is a discrete variable, BB84 is an example of a discrete-variable quantum key distribution (DV-QKD) scheme. BB84 is also an example of a prepare-and-measure protocol, because of the preparation action of 👩 Alice and the measurement action of 🧔 Bob. Classical post-processing phaseThis phase of the protocol involves 👩 Alice and 🧔 Bob exchanging a sequence of classical information in the classical channel to transform their raw key pair into a shared secret key [Wol21, Sec. 1.3.3]:
Table 1 shows an example of an exchange between 👩 Alice and 🧔 Bob in the absence of eavesdropping. For discussion of physical realisations of BB84, follow this knowledge base entry. Performance and security evaluationIn terms of performance, a basic figure of merit of every QKD protocol is the secret key rate, i.e. the fraction of secure key bits produced per protocol round. For security, follow this overview of QKD security. References
| ||||||||||||||||||||||||||||
BB84: Physical realisations | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Acknowledgement: Andrew Edwards contributed some explanation.
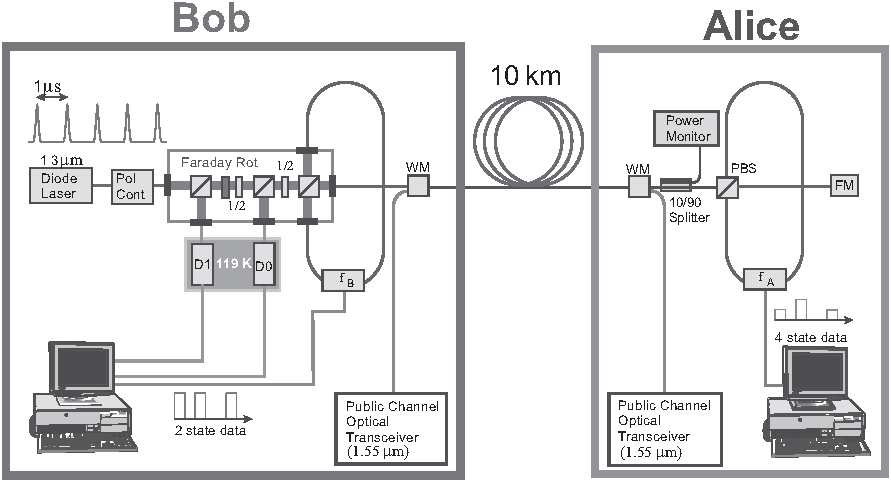
Continuing from an overview of BB84, this entry discusses several ways in which BB84 can be realised. Fig. 1 shows an experimental setup built by IBM [NC10, Box 12.7], where
For the setup in Fig. 1,
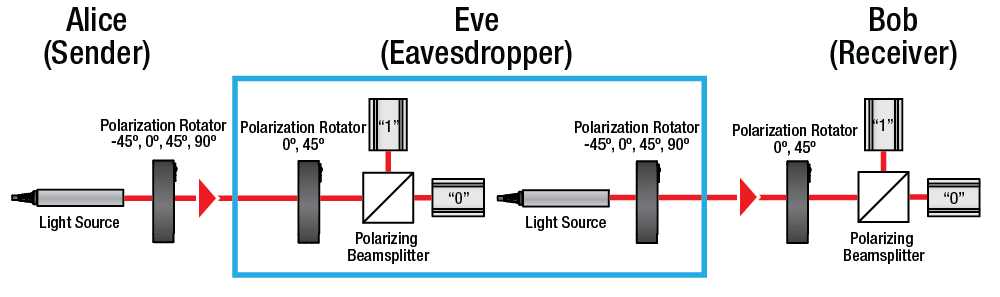
Fig. 2 shows a minimalist block diagram for EDU-QCRY1, while Fig. 3 shows a photo of a physical setup realising the block diagram. Let us study the functions of the PBS in this context:
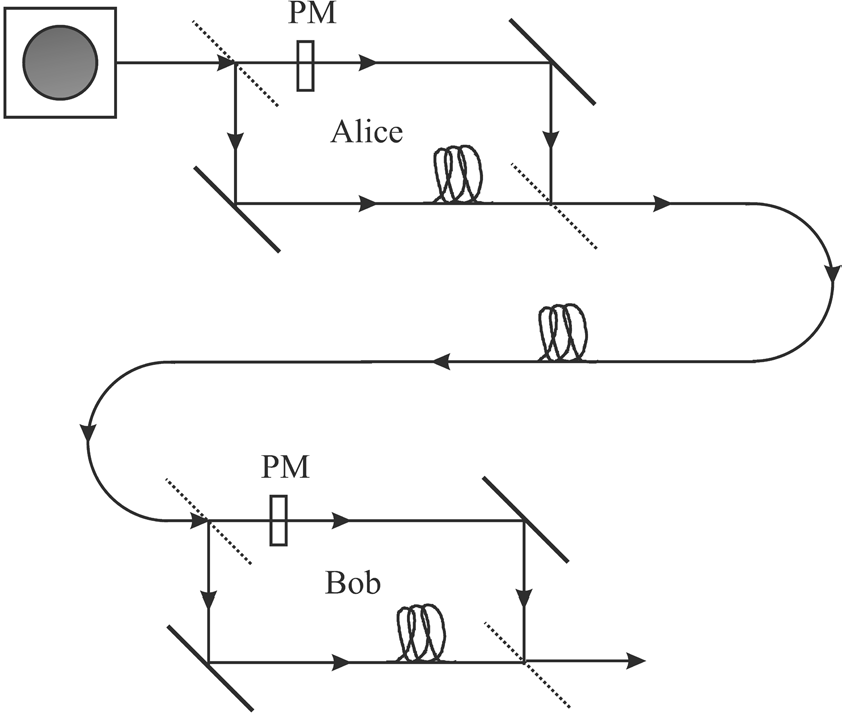
In recent years, satellite-based experiments on BB84 and extensions of BB84 (e.g., decoy-state BB84) had been conducted [LCPP22]. Compared to free space, polarisation is harder to preserve over commercial optical fibres [GK05, Fig. 11.7]. An alternative approach to polarisation is using an interferometer, such as a Mach-Zehnder interferometer; see Fig. 7 and [HIP+21, Sec. 3.2]. References
| ||||||||||||||
Bell states | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
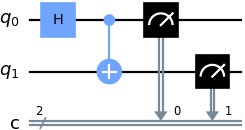
Consider the circuit below, where a Hadamard gate is connected to qubit and a controlled-NOT (CNOT) gate is connected to after the Hadamard gate: The Hadamard gate in Fig. 1 effects the transformations: and . The CNOT gate in Fig. 1 has its control qubit connected to the line, and its target qubit connected to the line. The unitary matrix representing the CNOT gate is If the input to the CNOT gate is the state , then the output is Thus, as an example, if the input is , then the Hadamard gate transforms it to , and the CNOT gate further transforms it to Table 1 is the truth table summarising the outputs corresponding to basis-state inputs.
The output states in Table 1 are called the Bell states or Einstein-Podolsky-Rosen (EPR) pairs [KLM07, p. 75; NC10, Sec. 1.3.6], and can be represented concisely as When the Bell states are used as an orthonormal basis, they are called the Bell basis [Wil17, pp. 91-93]. References
| ||||||||||||||||||
Bloch sphere | ||||||
|---|---|---|---|---|---|---|
Consider the ket vector , where and are complex-valued probability amplitudes, and are the computational bases. We can express and in the exponential form [Wil17, (3.6)]: Thus, given , we can rewrite it in the physically equivalent form: 💡 Above, is used instead of because for visualisation using a Bloch sphere (more on this later), as ranges from 0 to , the values of and are confined within to ensure the qubit representation is unique [Wil17, p. 57]. So what is a Bloch sphere? Named after physicist Felix Bloch, a Bloch sphere is a unit-radius sphere for visualising a qubit relative to the computational basis states. As shown in Fig. 1,
As explained in Fig. 2, a sphere provides the necessary number of degrees of freedom to represent a ket vector. The equator of a Bloch sphere enables the representation of complementary bases. For example, in Fig. 3,
References
| ||||||
C |
|---|
Coherent attack | |||
|---|---|---|---|
The discussion here follows from the discussion of collective attacks. | |||
Coherent state | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
A coherent state is a special quantum state that a coherent laser ideally emits [Wil07, p. 19]. That 👆 does not say much, but there is no straightforward way to define “coherent state”, a concept introduced by Schrödinger [SZ97, p. 46]. Mathematically and in short, a coherent state is the eigenstate of the positive frequency part of the electric field operator [SZ97, p. 46], but this requires definition of the electric field operator, which in turn requires discussion of the quantization of electromagnetic fields. Classically, an electromagnetic field consists of waves with well-defined amplitude and phase, but in quantum mechanics, this is no longer true. More precisely, there are fluctuations in both the amplitude and phase of the field [SZ97, Ch. 2]. A coherent state is a state that has the same fluctuations of quadrature amplitudes as the vacuum state but which possibly has nonzero average quadrature amplitudes [Van06, Sec. 4.6.1]. References
| ||||||||||
Collective attack | ||||||||
|---|---|---|---|---|---|---|---|---|
The discussion here follows from the discussion of individual attacks. In a collective attack [Sch10],
References
| ||||||||




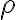



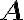
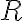












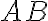
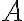
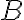






























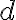




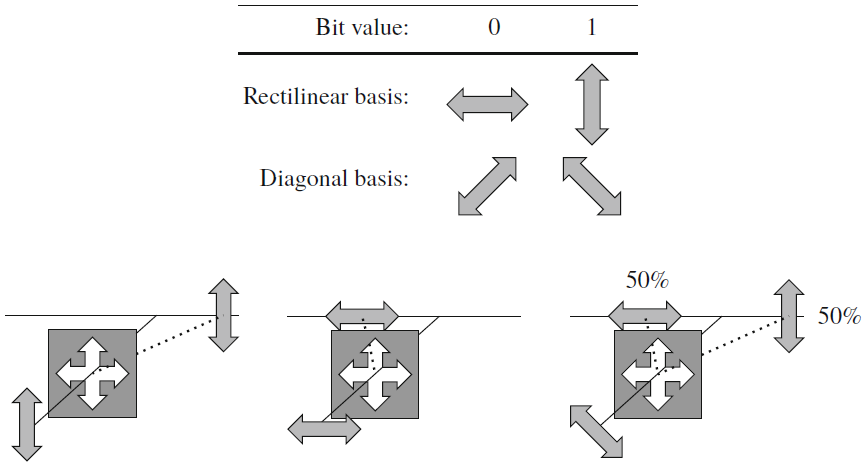
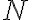

![\vec{X}=[X_1,\ldots,X_N] \vec{X}=[X_1,\ldots,X_N]](https://lo.unisa.edu.au/filter/tex/pix.php/2515a83a470bdbcc029cc2b4ebedaeff.gif)
![\vec{Y}=[Y_1,\ldots,Y_N] \vec{Y}=[Y_1,\ldots,Y_N]](https://lo.unisa.edu.au/filter/tex/pix.php/86ea149179c5dc6d91cf583a6fcbbd67.gif)


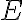


























![|\beta_{xy}\rangle = \frac{1}{\sqrt{2}}\left[|0,y\rangle + (-1)^x|1,\bar{y}\rangle \right]. |\beta_{xy}\rangle = \frac{1}{\sqrt{2}}\left[|0,y\rangle + (-1)^x|1,\bar{y}\rangle \right].](https://lo.unisa.edu.au/filter/tex/pix.php/aeea825e0da3da854a369461caca16de.gif)

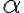
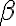



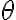

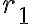







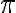
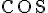
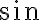
![[0,1] [0,1]](https://lo.unisa.edu.au/filter/tex/pix.php/ccfcd347d0bf65dc77afe01a3306a96b.gif)