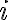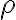Browse the glossary using this index

Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL

Projective measurement

by Yee Wei Law - Sunday, 4 June 2023, 12:31 PM

The discussion here follows from the discussion of the positive operator-valued measure (POVM).

The POVM cannot be used to determine the post-measurement state because the post-measurement state may not be pure [WN17, p. 13]. Instead, a Kraus operator representation of the POVM, known as projective measurement, is necessary to specify the post-measurement state.

Projective measurements are repeatable, and the outcome observed as a result of projective measurement is deterministic [MM12, Sec. 2.7], as explained below.

⚠	This repeatability implies many important measurements in quantum mechanics are not projective measurements; for instance, if we use a silvered screen to measure the position of a photon, we destroy the photon in the process, and obviously this measurement cannot be repeated.

Projective measurements are often discussed in terms of an observable, which is defined as a Hermitian operator acting on the state space of a system.

Every observable $\mathbf{M}$ has a spectral decomposition [Mey00, p. 517]:

$\mathbf{M} = \sum_i\lambda_i\mathbf{M}_i,$

where $\lambda_i$ are the eigenvalues of $\mathbf{M}$ , and $\mathbf{M}_i$ are so-called spectral/orthogonal projectors onto the null space of $(\mathbf{M}-\lambda_i\mathbf{I})$ . More precisely, 1️⃣ $\mathbf{M}_i$ are Hermitian and idempotent, 2️⃣ $\sum_i\mathbf{M}_i=\mathbf{I}$ , and 3️⃣ $\mathbf{M}_i$ are mutually orthogonal.

Clearly, $\mathbf{M}_i$ are valid POVM elements.

A (non-unique) Kraus operator representation or Kraus decomposition of $\mathbf{M}$ is defined as [WN17, Definition 1.5.2]:

$\mathbf{M} = \sum_i\lambda_i\mathbf{A}_i^\dagger\mathbf{A}_i,$

where $\mathbf{A}_i^\dagger\mathbf{A}_i = \mathbf{M}_i$ .

If we define $\mathbf{A}_i\triangleq\mathbf{M}_i$ , then $\mathbf{A}_i^\dagger\mathbf{A}_i = \mathbf{M}_i^\dagger\mathbf{M}_i = \mathbf{M}_i^2 = \mathbf{M}_i$ .
If we define $\mathbf{A}_i\triangleq\mathbf{U}\sqrt{\mathbf{M}_i}$ , where $\mathbf{U}$ is any unitary matrix, then $\mathbf{A}_i^\dagger\mathbf{A}_i = \sqrt{\mathbf{M}_i}^\dagger\mathbf{U}^\dagger\mathbf{U}\sqrt{\mathbf{M}_i} = \mathbf{M}_i$ .
Thus, there is no unique Kraus representation/decomposition.

With Kraus operators, we can now define projective measurement:

Definition 1: Projective measurement [WN17, Definition 1.5.4; MM12, p. 153]

A projective measurement is given by a set of orthogonal projectors $\mathbf{M}_i$ such that $\sum_i\mathbf{M}_i=\mathbf{I}$ . By default, the Kraus operator is chosen to be $\mathbf{A}_i = \mathbf{M}_i$ .

The probability of observing measurement outcome $i$ given initial state $\rho$ is

$\Pr\{i|\rho\} = \text{tr}(\mathbf{A}_i\rho).$

The post-measurement state is

$\rho' = \dfrac{\mathbf{A}_i\rho\mathbf{A}_i}{\text{tr}(\mathbf{A}_i\rho)}.$

For pure state $\rho=|\psi\rangle\langle\psi|$ , the post-measurement state is

$|\psi'\rangle=\dfrac{\mathbf{A}_i|\psi\rangle}{\sqrt{\langle\psi|\mathbf{A}_i|\psi\rangle}}.$

⚠	Most authors equate the term “von Neumann measurement” to “projective measurement”, but some consider the former to be a special case of the latter [KLM07, p.50].

Since the default Kraus operators are the same as the orthogonal projectors, most authors skip discussion of Kraus operators altogether 🤷‍♂️.

Measuring the observable $\mathbf{M}$ is equivalent to performing a projective measurement with respect to the decomposition $\mathbf{I} = \sum_i\mathbf{M}_i$ , where the measurement outcome $i$ corresponds to eigenvalue $\lambda_i$ .

Example 1 [KLM07, Example 3.4.1]

Consider the Pauli observable $\mathbf{Z}$ , i.e., the Pauli-Z operator/matrix:

$\mathbf{Z} = \begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix},$

which does not change an input of $|0\rangle$ , but flips $|1\rangle$ to $-|1\rangle$ (which is equivalent to $|1\rangle$ with a phase change).

The Pauli-Z operator acts as a NOT operator in the Hadamard basis.

$\mathbf{Z}$ has eigenpairs $(1, |0\rangle)$ and $(-1, |1\rangle)$ , where the eigenvectors $|0\rangle$ and $|1\rangle$ are also called eigenstates [MM12, p. 338].

Thus, $\mathbf{Z}$ has spectral decomposition:

$\mathbf{Z} = \begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix} = |0\rangle\langle0| - |1\rangle\langle1|,$

with orthogonal projectors

$\mathbf{M}_0 = |0\rangle\langle0|, \qquad \mathbf{M}_1 = |1\rangle\langle1|.$

Interpreting the above, a projective measurement of $\mathbf{Z}$ is a measurement in the standard basis with eigenvalue $1$ corresponding to final state $|0\rangle$ and eigenvalue $-1$ corresponding to final state $|1\rangle$ .

Example 2 [WN17, Example 1.5.3]

Given a two-qubit state $\rho$ , suppose we want to measure the parity of the two qubits in the standard basis.

One method is to measure $\rho$ in the ( $2^2$ -dimensional) standard basis, obtain two classical bits, and take their parity.

In this case, the probability of obtaining outcome “even” is

$\Pr\{\text{even}\} = \langle00|\rho|00\rangle + \langle11|\rho|11\rangle,$

and the post-measurement state is

Another method is to measure the parity using projective measurement which directly projects $\rho$ onto the relevant subspaces, without measuring the qubits individually. Define projectors:

$\mathbf{A}_{\text{even}} = |00\rangle\langle00| + |11\rangle\langle11|, \qquad \mathbf{A}_{\text{odd}} = \mathbf{I} - \mathbf{A}_{\text{even}} = |01\rangle\langle01| + |10\rangle\langle10|,$

which we can quickly verify to be orthogonal and conformant with the completeness relation:

$\mathbf{A}_{\text{even}}^\dagger\mathbf{A}_{\text{odd}} = 0, \qquad \mathbf{A}_{\text{even}} + \mathbf{A}_{\text{odd}} = \mathbf{I}.$

In this case, the probability of getting outcome “even” is

$\begin{split}\Pr\{\text{even}\} &= \text{tr}\{\mathbf{A}_{\text{even}}\rho\} = \text{tr}\{(|00\rangle\langle00| + |11\rangle\langle11|)\rho\} \\ &= \text{tr}\{|00\rangle\langle00|\rho\} + \text{tr}\{|11\rangle\langle11|\rho\} = \text{tr}\{\langle00|\rho|00\rangle\} + \text{tr}\{\langle11|\rho|11\rangle\} \\ &= \langle00|\rho|00\rangle + \langle11|\rho|11\rangle,\end{split}$

which is the same as before; and the post-measurement state is

$\rho' = \dfrac{\mathbf{A}_{\text{even}}\rho\mathbf{A}_{\text{even}}}{\langle00|\rho|00\rangle + \langle11|\rho|11\rangle}.$

The preceding two methods produce different outcomes on the EPR state $|\text{EPR}\rangle \triangleq \dfrac{1}{\sqrt{2}}(|00\rangle + |11\rangle)$ , or in density-matrix representation,

$\rho_\text{EPR} = |\text{EPR}\rangle\langle\text{EPR}| = \dfrac{1}{2}(|00\rangle\langle00| + |11\rangle\langle11| + |00\rangle\langle11| + |11\rangle\langle00|).$

By measurement in the standard basis, the probability of getting outcome “even” is

$\begin{split} \Pr\{\text{even}\} &= \langle00|\rho_{\text{EPR}}|00\rangle + \langle11|\rho_{\text{EPR}}|11\rangle \\ &= \dfrac{1}{2}\langle00|(|00\rangle\langle00| + |11\rangle\langle11| + |00\rangle\langle11| + |11\rangle\langle00|)|00\rangle + \langle11|\rho_{\text{EPR}}|11\rangle \\ &= \dfrac{1}{2}(\langle00| + \langle11|)|00\rangle + \langle11|\rho_{\text{EPR}}|11\rangle = \dfrac{1}{2} + \dfrac{1}{2} = 1, \end{split}$

while the post-measurement state is

$\rho' = \langle00|\rho|00\rangle|00\rangle\langle00| + \langle11|\rho|11\rangle|11\rangle\langle11| = \dfrac{1}{2}|00\rangle\langle00| + \dfrac{1}{2}|11\rangle\langle11|.$

By projective measurement, $\Pr\{\text{even}\}$ is the same as before, but the post-measurement state is different:

Thus, projective measurement with $\mathbf{A}_{\text{even}}$ does not change the EPR state.

This is one of the main advantages of using projective measurement as opposed to basis measurement: the former enables simple computation (e.g., parity) on multi-qubit states without fully “destroying” the state, as basis measurement does.

In Example 2, the observation that the projective measurement preserves the quantum state is not a coincidence. In fact, building on Definition 1, applying measurement $\mathbf{A}_i$ to $|\psi'\rangle$ , i.e., applying $\mathbf{A}_i$ to $|\psi\rangle$ twice gives us [MM12, p. 153]:

$\begin{split} |\psi''\rangle = \dfrac{\mathbf{A}_i|\psi'\rangle}{\sqrt{\langle\psi'|\mathbf{A}_i|\psi'\rangle}} = \dfrac{\mathbf{A}_i|\psi\rangle}{\sqrt{\langle\psi'|\mathbf{A}_i|\psi'\rangle\langle\psi|\mathbf{A}_i|\psi\rangle}} = \dfrac{\mathbf{A}_i|\psi\rangle}{\sqrt{\frac{\langle\psi|\mathbf{A}^\dagger_i}{\sqrt{p_i}}\mathbf{A}_i\frac{\mathbf{A}_i|\psi\rangle}{\sqrt{p_i}}p_i}} = |\psi'\rangle, \end{split}$

where $p_i\triangleq\langle\psi|\mathbf{A}_i|\psi\rangle$ .

References

[KLM07]	P. Kaye, R. Laflamme, and M. Mosca, An Introduction to Quantum Computing, Oxford University Press, 2007. Available at https://ebookcentral.proquest.com/lib/unisa/reader.action?docID=415080.
[MM12]	D. C. Marinescu and G. M. Marinescu, Classical and Quantum Information, Elsevier, 2012. https://doi.org/10.1016/C2009-0-64195-7.
[Mey00]	C. Meyer, Matrix Analysis and Applied Linear Algebra, SIAM, 2000. Available at http://portal.igpublish.com.eu1.proxy.openathens.net/iglibrary/obj/SIAMB0000114.
[NC10]	M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information, 10th anniversary ed., Cambridge University Press, 2010. Available at http://mmrc.amss.cas.cn/tlb/201702/W020170224608149940643.pdf.
[WN17]	S. Wehner and N. Ng, Lecture Notes: edX Quantum Cryptography, CaltechDelftX: QuCryptox, 2017. Available at https://courses.edx.org/courses/course-v1:CaltechDelftX+QuCryptox+3T2018/pdfbook/0/.

Keyword(s):

Cyber Engineering Knowledge Base

Math and physics (including quantum)

Projective measurement

References