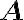Browse the glossary using this index
Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
Idempotence | ||||||||
|---|---|---|---|---|---|---|---|---|
A square matrix, , is idempotent if it is equal to its square, i.e., [Ber18, Definition 4.1.1]. Notable properties: References
| ||||||||