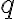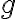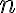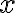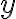The Diffie-Hellman (D-H) key agreement (often called “key exchange”) protocol is standardised in NIST SP 800-56A [BCR+18].

The protocol originated in the seminal 1976 paper by Whitfield Diffie and Martin Hellman [DH76], both recipients of the 2016 Turing Award (their contribution took 40 years to be recognised).

Protocol between 👩 Alice and 🧔 Bob [KL21, CONSTRUCTION 11.2] in Fig. 1:

1. On input of security parameter $1^n$, 👩 Alice runs probabilistic polynomial-time (PPT) algorithm to obtain the domain parameters $(\mathbb{G}, q, g)$, where $\mathbb{G}$ is a cyclic group of prime order $q$, and $g$ is a generator of $\mathbb{G}$.

   The bit-length of $q$ = the security parameter $n$.

   The domain parameters can be pre-distributed.

2. 👩 Alice chooses $x\in\mathbb{Z}_q$, $0\lt x\lt q$, uniformly at random, and computes $h_A \gets g^x$.

   $\mathbb{Z}_q$ is the (cyclic) group of integers modulo $q$.

   👩 Alice’s (ephemeral) private key and public key are $x$ and $g^x$ respectively.

3. 👩 Alice sends $(\mathbb{G}, q, g, h_A)$ to 🧔 Bob.

4. 🧔 Bob chooses $y\in\mathbb{Z}_q$, $0\lt y\lt q$,  uniformly at random, and computes $h_B \gets g^y$.

   🧔 Bob’s (ephemeral) private key and public key are $y$ and $g^y$ respectively.

5. 🧔 Bob sends $h_B$ to 👩 Alice and outputs $k_B \gets h_A^y$.
6. 👩 Alice computes $k_A \gets h_B^x$.

Successful completion of the protocol results in the session key $k_A = k_B = g^{xy}$.

A necessary condition for preventing a probabilistic polynomial-time (PPT) eavesdropper from computing the session key is that the computational Diffie-Hellman (CDH) problem is hard:

However, the hardness of the CDH problem is not sufficient.

Just as indistinguishability plays an essential role in symmetric-key encryption, indistinguishability is key here: if the session key $g^{xy}$ is indistinguishable from an element chosen uniformly at random from $\mathbb{G}$, then we have a sufficient condition for preventing a PPT eavesdropper from computing the session key [KL21, pp. 393-394].

The indistinguishability condition is equivalent to the assumption that the decisional Diffie-Hellman (DDH) problem is hard:

The DDH problem is readily reducible to the CDH problem, since any algorithm that solves the CDH can compute $g^{xy}$ and compare it with $g^z$; implying the DDH problem is no harder than the CDH problem.

In turn, the CDH problem is reducible to the discrete logarithm problem (DLP, see Definition 3), since any algorithm that solves the DLP can compute $x$ from $g^x$, $y$ from $g^y$, and hence $g^{xy}$; implying the CDH problem is no harder than the DLP problem.

In other words, the DDH problem can be reduced to the CDH problem, which in turn can be reduced to the DLP; solving the DLP breaks the D-H key agreement protocol.

The D-H key agreement protocol is used in the Internet Key Exchange (IKE) protocol, which is currently at version 2 [KHN+14].