Browse the glossary using this index
Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
Spectral theorem and spectral decomposition | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Spectral theorem is one of the fundamental theorems of linear algebra [ABH09, Sec. 3.6]. Based on the spectral theorem, spectral decomposition is an essential tool in quantum theory [NC10, Box 2.2]. Multiple equivalent interpretations of the spectral theorem exist, e.g., [ABH09, Theorems 3.6.4 and 3.6.12]. The interpretation in Theorem 1 directly defines spectral decomposition, and is hence also called the spectral decomposition theorem. Theorem 1: Spectral (decomposition) theorem [Hol13, Theorem 8.23; Zha11, Theorem 3.4; KLM07, Theorem 2.4.3]
Any normal operator, , has an outer product representation [KLM07, Sec. 2.4; Mey00, p. 517]: where The outer products are projectors that satisfy
References
| ||||||||||||||
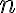
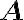
















![(1, 1/\sqrt{2}[1 \; 1]^\top) (1, 1/\sqrt{2}[1 \; 1]^\top)](https://lo.unisa.edu.au/filter/tex/pix.php/3d5f032860eb51fb9bb5b31778fedd2e.gif)
![(-1, 1/\sqrt{2}[-1 \; 1]^\top) (-1, 1/\sqrt{2}[-1 \; 1]^\top)](https://lo.unisa.edu.au/filter/tex/pix.php/302a8b3e6ef008ebe240fe4692b4d52f.gif)
