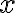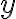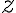Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
B |
|---|
BB84: Overview | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Quantum key distribution (QKD) is a method for generating and distributing symmetric cryptographic keys with information-theoretic security based on quantum information theory [ETS18]. A QKD protocol establishes a secret key between two parties — let us call them 👩 Alice and 🧔 Bob as per tradition — connected by 1️⃣ an insecure quantum channel and 2️⃣ an authenticated classical channel [Gra21, Sec. 3.1].
A QKD protocol typically proceeds in two phases [Wol21, Ch. 4]:
The security of QKD hinges on the principles of quantum mechanics, rather than the hardness of any computational problem, and hence does not get threatened by advances in computing technologies.
Theorem 1: No-cloning theorem [WZ82]
It is not possible to perfectly clone an unknown quantum state. The earliest QKD protocol is due to Bennett and Brassad [BB84] and is called BB84, named after the authors and the year it was proposed. QKD leverages physical mechanisms, so unavoidably we need to discuss the physical mechanisms that underlie/enable BB84, which are based primarily on the polarisation of photons [Wol21, Sec. 1.3.1]. PolarisationThe polarisation of photons specifies the geometrical orientation of the oscillation of its electromagnetic field.
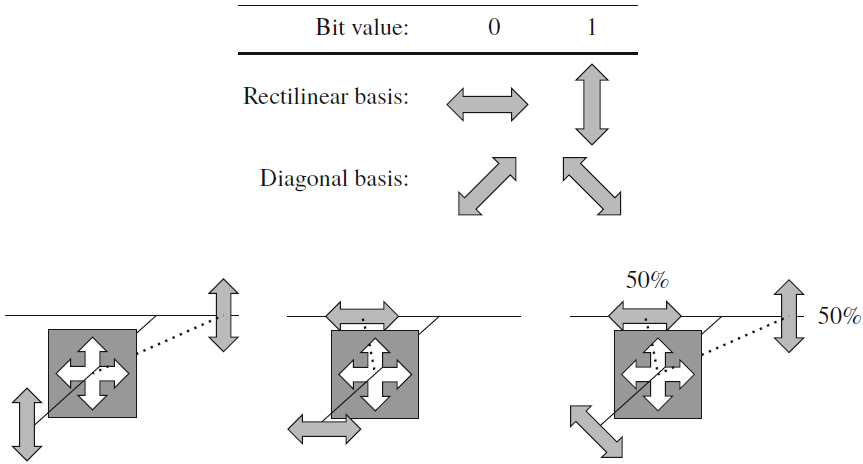
We only consider linear polarisation here. For linear polarisation, we distinguish between two bases:
Consider the effect of polarisation filters depicted in Fig. 1:
Thus, measuring a diagonally polarised photon in the rectilinear basis, and similarly measuring a vertically/horizontally polarised photon in the diagonal basis, give a random result.
With knowledge of polarisation in mind, let us now discuss the quantum transmission phase of BB84, which involves encoding of classical bits into quantum states, communication over a quantum channel, and decoding of quantum states into classical bits. Quantum transmission phaseThis phase of the protocol involving 👩 Alice and 🧔 Bob goes like this [Wol21, Sec. 1.3.2]:
An illustration of the process above can be found Fig. 1. Since the polarisation state of each photon is a discrete variable, BB84 is an example of a discrete-variable quantum key distribution (DV-QKD) scheme. BB84 is also an example of a prepare-and-measure protocol, because of the preparation action of 👩 Alice and the measurement action of 🧔 Bob. Classical post-processing phaseThis phase of the protocol involves 👩 Alice and 🧔 Bob exchanging a sequence of classical information in the classical channel to transform their raw key pair into a shared secret key [Wol21, Sec. 1.3.3]:
Table 1 shows an example of an exchange between 👩 Alice and 🧔 Bob in the absence of eavesdropping. For discussion of physical realisations of BB84, follow this knowledge base entry. Performance and security evaluationIn terms of performance, a basic figure of merit of every QKD protocol is the secret key rate, i.e. the fraction of secure key bits produced per protocol round. For security, follow this overview of QKD security. References
| ||||||||||||||||||||||||||||
BB84: Physical realisations | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Acknowledgement: Andrew Edwards contributed some explanation.
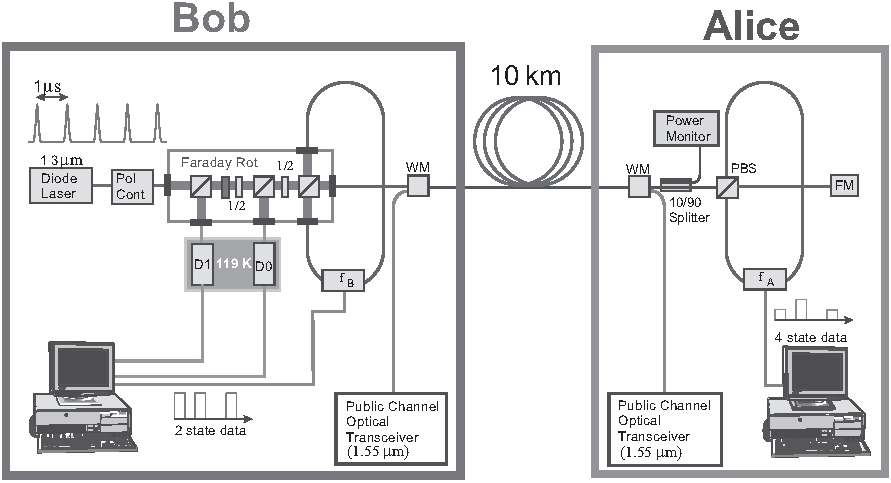
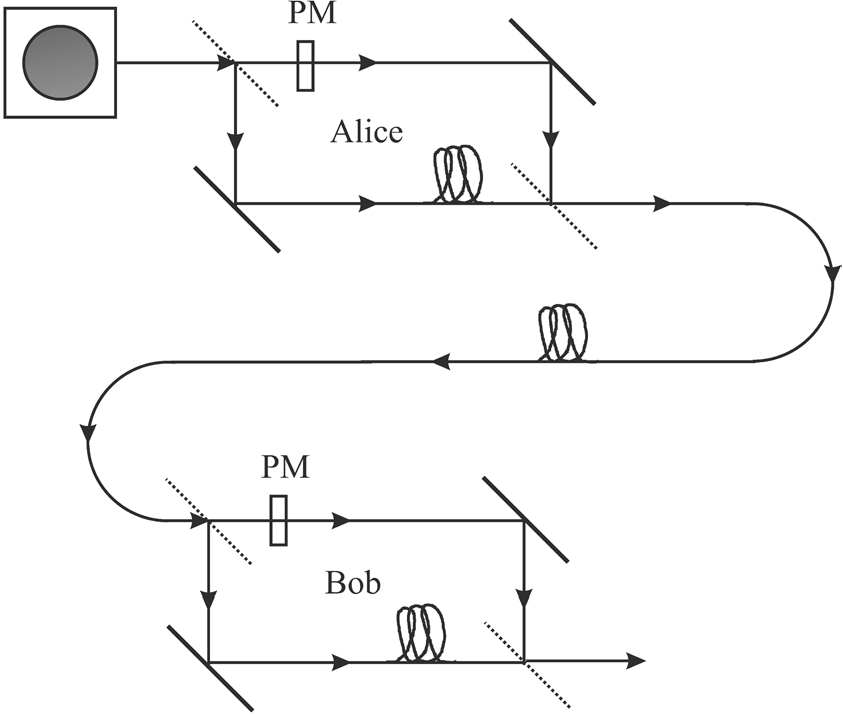
Continuing from an overview of BB84, this entry discusses several ways in which BB84 can be realised. Fig. 1 shows an experimental setup built by IBM [NC10, Box 12.7], where
For the setup in Fig. 1,
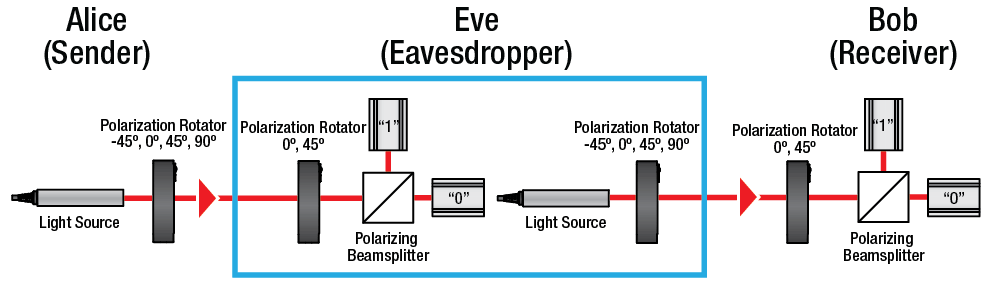
Fig. 2 shows a minimalist block diagram for EDU-QCRY1, while Fig. 3 shows a photo of a physical setup realising the block diagram. Let us study the functions of the PBS in this context:
In recent years, satellite-based experiments on BB84 and extensions of BB84 (e.g., decoy-state BB84) had been conducted [LCPP22]. Compared to free space, polarisation is harder to preserve over commercial optical fibres [GK05, Fig. 11.7]. An alternative approach to polarisation is using an interferometer, such as a Mach-Zehnder interferometer; see Fig. 7 and [HIP+21, Sec. 3.2]. References
| ||||||||||||||
Bell states | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
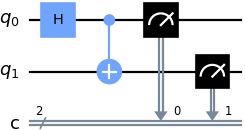
Consider the circuit below, where a Hadamard gate is connected to qubit and a controlled-NOT (CNOT) gate is connected to after the Hadamard gate: The Hadamard gate in Fig. 1 effects the transformations: and . The CNOT gate in Fig. 1 has its control qubit connected to the line, and its target qubit connected to the line. The unitary matrix representing the CNOT gate is If the input to the CNOT gate is the state , then the output is Thus, as an example, if the input is , then the Hadamard gate transforms it to , and the CNOT gate further transforms it to Table 1 is the truth table summarising the outputs corresponding to basis-state inputs.
The output states in Table 1 are called the Bell states or Einstein-Podolsky-Rosen (EPR) pairs [KLM07, p. 75; NC10, Sec. 1.3.6], and can be represented concisely as When the Bell states are used as an orthonormal basis, they are called the Bell basis [Wil17, pp. 91-93]. References
| ||||||||||||||||||
Bloch sphere | ||||||
|---|---|---|---|---|---|---|
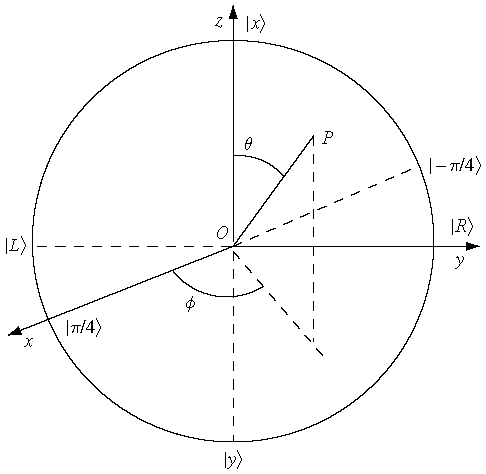
Consider the ket vector , where and are complex-valued probability amplitudes, and are the computational bases. We can express and in the exponential form [Wil17, (3.6)]: Thus, given , we can rewrite it in the physically equivalent form: 💡 Above, is used instead of because for visualisation using a Bloch sphere (more on this later), as ranges from 0 to , the values of and are confined within to ensure the qubit representation is unique [Wil17, p. 57]. So what is a Bloch sphere? Named after physicist Felix Bloch, a Bloch sphere is a unit-radius sphere for visualising a qubit relative to the computational basis states. As shown in Fig. 1,
As explained in Fig. 2, a sphere provides the necessary number of degrees of freedom to represent a ket vector. The equator of a Bloch sphere enables the representation of complementary bases. For example, in Fig. 3,
References
| ||||||

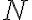

![\vec{X}=[X_1,\ldots,X_N] \vec{X}=[X_1,\ldots,X_N]](https://lo.unisa.edu.au/filter/tex/pix.php/2515a83a470bdbcc029cc2b4ebedaeff.gif)
![\vec{Y}=[Y_1,\ldots,Y_N] \vec{Y}=[Y_1,\ldots,Y_N]](https://lo.unisa.edu.au/filter/tex/pix.php/86ea149179c5dc6d91cf583a6fcbbd67.gif)




























![|\beta_{xy}\rangle = \frac{1}{\sqrt{2}}\left[|0,y\rangle + (-1)^x|1,\bar{y}\rangle \right]. |\beta_{xy}\rangle = \frac{1}{\sqrt{2}}\left[|0,y\rangle + (-1)^x|1,\bar{y}\rangle \right].](https://lo.unisa.edu.au/filter/tex/pix.php/aeea825e0da3da854a369461caca16de.gif)

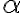
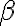



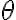

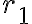







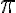
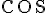
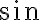
![[0,1] [0,1]](https://lo.unisa.edu.au/filter/tex/pix.php/ccfcd347d0bf65dc77afe01a3306a96b.gif)