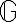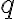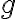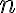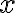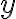Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
D |
|---|
Data flow analysis | ||||||
|---|---|---|---|---|---|---|
This continues from discussion of application security testing. Data flow analysis is a static analysis technique for calculating facts of interest at each program point, based on the control flow graph representation of the program [vJ11, p. 1254]. A canonical data flow analysis is reaching definitions analysis [NNH99, Sec. 2.1.2]. For example, if statement is Reaching definitions analysis determines for each statement that uses variable Example 1 [vJ11, pp. 1254-1255]
In the example below, the definition
x at line 1 reaches line 2, but does not reach beyond line 3 because x is assigned on line 3.
More formally, data flow analysis can be expressed in terms of lattice theory, where facts about a program are modelled as vertices in a lattice. The lattice meet operator determines how two sets of facts are combined. Given an analysis where the lattice meet operator is well-defined and the lattice is of finite height, a data flow analysis is guaranteed to terminate and converge to an answer for each statement in the program using a simple iterative algorithm. A typical application of data flow analysis to security is to determine whether a particular program variable is derived from user input (tainted) or not (untainted). Given an initial set of variables initialised by user input, data flow analysis can determine (typically an over approximation of) all variables in the program that are derived from user data. References
| ||||||
Delay-tolerant networking (DTN) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
In a mobile ad hoc network (MANET, see Definition 1), nodes move around causing connections to form and break over time. Definition 1: Mobile ad hoc network [PBB+17]
A wireless network that allows easy connection establishment between mobile wireless client devices in the same physical area without the use of an infrastructure device, such as an access point or a base station. Due to mobility, a node can sometimes find itself devoid of network neighbours. In this case, the node 1️⃣ stores the messages en route to their destination (which is not the node itself), and 2️⃣ when it finds a route of the destination of the messages, forwards the messages to the next node on the route. This networking paradigm is called store-and-forward. A delay-tolerant networking (DTN) architecture [CBH+07] is a store-and-forward communications architecture in which source nodes send DTN bundles through a network to destination nodes. In a DTN architecture, nodes use the Bundle Protocol (BP) to deliver data across multiple links to the destination nodes. Watch short animation from NASA: Watch detailed lecture from NASA: References
| ||||||||||||
Differential power analysis | ||||
|---|---|---|---|---|
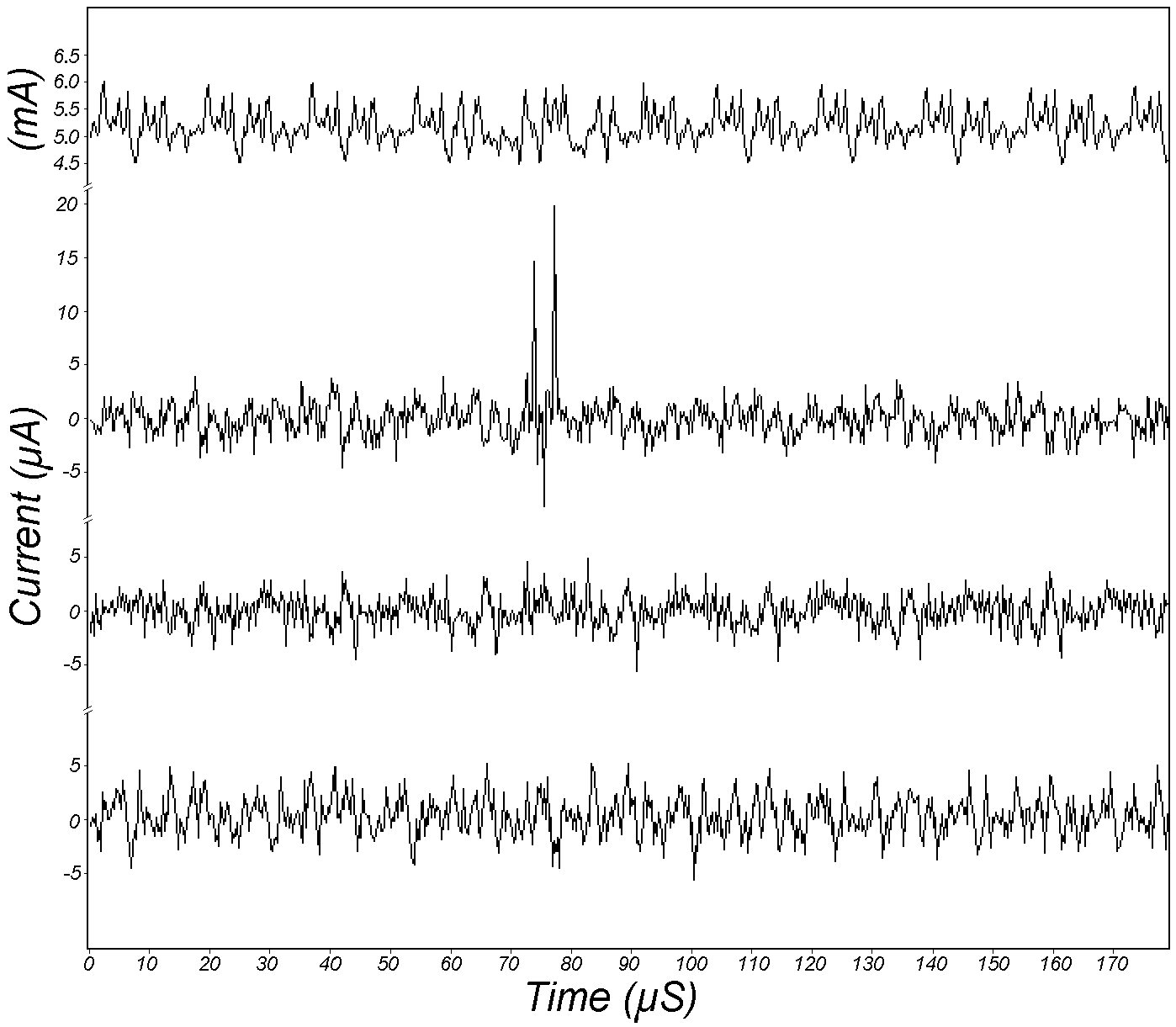
Kocher et al. [KJJ99] pioneered the method of differential power analysis (DPA). A power trace is a set of power consumption measurements taken over a cryptographic operation; see Fig. 1 for an example. Let us define simple power analysis (SPA) before we get into DPA. SPA is the interpretation of direct power consumption measurements of cryptographic operations like Fig. 1. Watch a demonstration of SPA: Most hard-wired hardware implementations of symmetric cryptographic algorithms have sufficiently small power consumption variations that SPA cannot reveal any key bit. Unlike SPA, DPA is the interpretation of the difference between two sets of power traces. More precisely, this difference is defined as where
Note each trace is associated with a different ciphertext. ⚠ DPA was originally devised for DES but it can be adapted to other cryptographic algorithms. DPA uses power consumption measurements to determine whether a key block guess is correct.
References
| ||||
Diffie-Hellman key agreement | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
The Diffie-Hellman (D-H) key agreement (often called “key exchange”) protocol is standardised in NIST SP 800-56A [BCR+18]. The protocol originated in the seminal 1976 paper by Whitfield Diffie and Martin Hellman [DH76], both recipients of the 2016 Turing Award (their contribution took 40 years to be recognised). Protocol between 👩 Alice and 🧔 Bob [KL21, CONSTRUCTION 11.2] in Fig. 1:
Successful completion of the protocol results in the session key . A necessary condition for preventing a probabilistic polynomial-time (PPT) eavesdropper from computing the session key is that the computational Diffie-Hellman (CDH) problem is hard: Definition 1: Computational Diffie-Hellman (CDH) problem [Gal12, Definition 20.2.1]
However, the hardness of the CDH problem is not sufficient. Just as indistinguishability plays an essential role in symmetric-key encryption, indistinguishability is key here: if the session key is indistinguishable from an element chosen uniformly at random from , then we have a sufficient condition for preventing a PPT eavesdropper from computing the session key [KL21, pp. 393-394]. The indistinguishability condition is equivalent to the assumption that the decisional Diffie-Hellman (DDH) problem is hard: Definition 2: Decisional Diffie-Hellman (DDH) problem [Gal12, Definition 20.2.3]
The DDH problem is readily reducible to the CDH problem, since any algorithm that solves the CDH can compute and compare it with ; implying the DDH problem is no harder than the CDH problem. In turn, the CDH problem is reducible to the discrete logarithm problem (DLP, see Definition 3), since any algorithm that solves the DLP can compute from , from , and hence ; implying the CDH problem is no harder than the DLP problem. Definition 3: Discrete logarithm problem (DLP) [Gal12, Definition 13.0.1]
In other words, the DDH problem can be reduced to the CDH problem, which in turn can be reduced to the DLP; solving the DLP breaks the D-H key agreement protocol. There are multiplicative groups for which the DLP is easy, so it is critical that the right groups are used. A safe-prime group is a cyclic subgroup of the Galois field with prime order , where is called a safe prime; this subgroup has elements [BCR+18, Sec. 5.5.1.1]. NIST [BCR+18, Appendix D] refers to RFC 3526 and RFC 7919 for definitions of safe-prime groups. The D-H key agreement protocol is used in the Internet Key Exchange (IKE) protocol, which is currently at version 2 [KHN+14]. References
| ||||||||||||
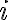
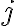
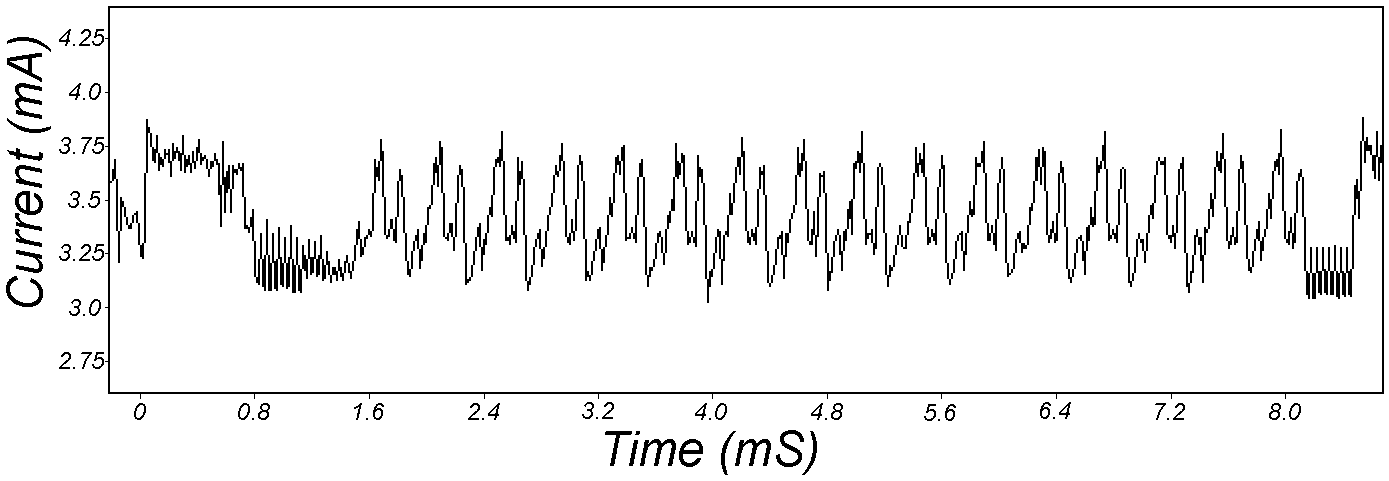
![\Delta_m[j] \triangleq \dfrac{\sum_{i=1}^m D(C_i,b,K_s)\vec{T}_i[j]}{\sum_{i=1}^m D(C_i,b,K_s)} - \dfrac{\sum_{i=1}^m [1-D(C_i,b,K_s)]\vec{T}_i[j]}{\sum_{i=1}^m [1-D(C_i,b,K_s)]}, \Delta_m[j] \triangleq \dfrac{\sum_{i=1}^m D(C_i,b,K_s)\vec{T}_i[j]}{\sum_{i=1}^m D(C_i,b,K_s)} - \dfrac{\sum_{i=1}^m [1-D(C_i,b,K_s)]\vec{T}_i[j]}{\sum_{i=1}^m [1-D(C_i,b,K_s)]},](https://lo.unisa.edu.au/filter/tex/pix.php/736d69d9fa8f066a9f809190f7c44753.gif)
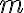

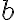

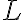


![\vec{T}_i[j] \vec{T}_i[j]](https://lo.unisa.edu.au/filter/tex/pix.php/61549829655dfd88a160b951b80f1094.gif)

![\lim_{m\to\infty}\Delta_m[j] = 0 \lim_{m\to\infty}\Delta_m[j] = 0](https://lo.unisa.edu.au/filter/tex/pix.php/c2639ccee60018577e6b520bb06d4b71.gif)
![\Delta_m[j_b] \Delta_m[j_b]](https://lo.unisa.edu.au/filter/tex/pix.php/a926c5e378adc9c88eaffff156066c43.gif)


![\Delta_m[j] \Delta_m[j]](https://lo.unisa.edu.au/filter/tex/pix.php/e2e2264203d8da66fd902df063843c28.gif)