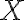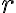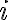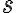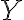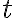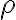The following introduces Shannon entropy before von Neumann entropy.

Shannon entropy

The Shannon entropy of a random variable, say $X$, measures the uncertainty of $X$.

Intuition:

• Minimum entropy occurs when $X$ takes on a specific value at probability 1. Let us say entropy is 0 in this case.
• Maximum entropy occurs when $X$ takes on one of $2^r$ different values at equal probability. Let us say entropy is $r$ bits in this case, because we need $r$ bits to represent all possible outcomes in binary.

The following definition of entropy, denoted by $H(X)$, measured in number of bits, can reflect the two extreme cases above [MC12, Definition 5.4]:

where $p_i$ denotes the probability of $X$ taking on the $i$th value.

⚠ Note: 1️⃣ $0\log_20\triangleq0$; 2️⃣ number of bits is discrete in practice but as a metric of comparison, we need entropy to be a continuous-valued metric.

If $X$ has $s$ possible values, and $Y$ has $t$, the joint entropy of $X$ and $Y$ is defined as [MC12, Definition 6.2]:

The conditional entropy of $X$ given $Y$ is defined as [MC12, (6.53)]:

$H(X|Y) \triangleq -\sum_{i=1}^s\sum_{j=1}^t \Pr_{X,Y}(x_i,y_j) \log_2 \Pr_{X|Y}(x_i|y_j).$

The chain rule for entropy states [MC12, p. 151; Gra21, (2.48)]:

or more generally,

Von Neumann entropy

The Shannon entropy measures the uncertainty associated with a classical probability distribution.

Quantum states are described in a similar fashion, with density operators replacing probability distributions.

The von Neumann entropy of a quantum state, $\rho$, is defined as [NC10, Sec. 11.3]:

$S(\rho) \triangleq -\text{tr}(\rho\log_2\rho),$

where $\log_2\rho$ denotes the base-2 logarithm of $\rho$ and not the element-wise application of base-2 logarithm to $\rho$.

Watch an introduction to the matrix logarithm on YouTube:

If $\lambda_i$ are the eigenvalues of $\rho$, then