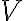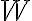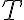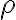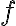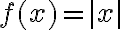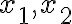Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
L |
|---|
Linear operator | ||||
|---|---|---|---|---|
Let and be vector spaces. The mapping is called a linear transformation if and only if
for every choice of and scalar . When , is called a linear operator [DG09, p. 202]. References
| ||||
Lipschitzness, Lipschitz condition | ||||||
|---|---|---|---|---|---|---|
Mathematical programming (theory-based optimisation methods as opposed to heuristics) works best with differentiable cost/loss functions. Mathematical programming also works with continuous loss functions [Byr15]. Differentiability implies continuity but the converse is not true, so continuity is a weaker condition than differentiability. For example, piecewise continuous functions are not differentiable at all points. Lipschitzness is a particular form of continuity. Strictly speaking, Lipschitzness is a form of uniform continuity: Definition 1: Lipschitzness [SSBD14, Definition 12.6]
Let . A function (in general, a mapping from one normed vector space to another) is -Lipschitz (continuous) over if for every , we have that
The preceding equation expresses the Lipschitzness or the Lipschitz condition of function . It follows from the definition above that if the derivative of is everywhere bounded in absolute value by , then is -Lipschitz. Example 1 [SSBD14, Example 12.4]
The function is 1-Lipschitz over because for every , the triangular inequality tells us
and similarly,
The two preceding equations combined give us . References
| ||||||
