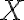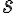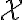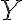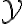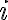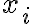Browse the glossary using this index

Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL

M

Mutual information

by Yee Wei Law - Monday, 27 March 2023, 3:18 PM

The following introduces classical mutual information before quantum mutual information.

Classical mutual information

Consider the channel model of a transmission system in Fig. 1.

Fig. 1: Channel model of a transmission system [MC12, Figure 6.3]. The input $X$ has $s$ possible values from the set $\mathcal{X}$ . The output $Y$ has $t$ possible values from the set $\mathcal{Y}$ .

Since the input takes a certain value at a certain probability, the input is a discrete random variable, which we denote by $X$ .

For the same reason, the output is also a discrete random variable, which we denote by $Y$ .
Watch Khan Academy’s video on random variables if you need a refresher.

Suppose the sender transmits the $i$ th input symbol as $x_i$ at a probability of $\Pr_X\{x_i\}$ , this probability is called the prior probability of $x_i$ .

“Prior probability” is often written in Latin as “a priori probability”.

Suppose the receiver receives $y_j$ as the $j$ th output symbol, the probability of this output conditioned on the $i$ th input being $x_i$ is the likelihood of $y_j$ : $\Pr_{Y|X}\{y_j|x_i\}$ .

However in most cases, we are more interested in the posterior probability of $x_i$ : $\Pr_{X|Y}\{x_i|y_j\}$ , i.e., what is the probability that the $i$ th input is $x_i$ given the $j$ th output is $y_j$ .

“Posterior probability” is often written in Latin as “a posteriori probability”.

The posterior probability helps us determine the amount of information that can be inferred about the input when the output takes a certain value.

The information gain or uncertainty loss about input $x_i$ upon receiving output $y_j$ is the mutual information of $x_i$ and $y_j$ , denoted by $I(x_i;y_j)$ [MC12, pp. 126-127].

$I(x_i;y_j)$ is thus the uncertainty in $x_i$ before receiving $y_j$ minus the uncertainty in $x_i$ after receiving $y_j$ .
The uncertainty in $x_i$ before receiving $y_j$ , measured in number of bits, is $\log_2\left(\frac{1}{\Pr_X\{x_i\}}\right)$ .
The uncertainty in $x_i$ after receiving $y_j$ , measured in number of bits, is $\log_2\left(\frac{1}{\Pr_{X|Y}\{x_i|y_j\}}\right)$ .
Thus,

$I(x_i;y_j) \triangleq \log_2\left(\frac{1}{\Pr_X\{x_i\}}\right) - \log_2\left(\frac{1}{\Pr_{X|Y}\{x_i|y_j\}}\right) = \log_2\left(\frac{\Pr_{X|Y}\{x_i|y_j\}}{\Pr_X\{x_i\}}\right).$
By Bayes’ Theorem, $\Pr_{X|Y}\{x_i|y_j\} = \Pr_{Y|X}\{y_j|x_i\}\Pr_X\{x_i\}/\Pr_Y\{y_j\}$ , so

$I(x_i;y_j) = \log_2\left(\frac{\Pr_{X|Y}\{x_i|y_j\}}{\Pr_X\{x_i\}}\right) = \log_2\left(\frac{\Pr_{Y|X}\{y_j|x_i\}}{\Pr_Y\{y_j\}}\right) = I(y_j;x_i),$

i.e., $x_i$ provides as much information about $y_j$ as $y_j$ does about $x_i$ .

If the events $X=x_i$ and $Y=y_j$ are independent, what is $I(x_i;y_j)$ ?

Extending the result above from $x_i$ to $X$ and from $y_j$ to $Y$ , we define the system/average mutual information of $X$ and $Y$ , denoted by $I(X;Y)$ , as the information gain or uncertainty loss about random variable $X$ by observing random variable $Y$ [MC12, Definition 6.7]:

$I(X;Y) \triangleq \sum_{i=1}^s\sum_{j=1}^t \Pr_{X,Y}(x_i,y_j)I(x_i;y_j).$

It is trivial to show that 1️⃣ $I(X;Y)=I(Y;X)$ , 2️⃣ $I(X;Y)\geq0$ , 3️⃣ $I(X;Y)=0$ iff $X$ and $Y$ are independent.

Omitting the derivation in [MC12, p. 129],

$I(X;Y) = H(X) + H(Y) - H(X,Y) = H(X) - H(X|Y) = H(Y) - H(Y|X),$

where $H(X)$ denotes the Shannon entropy of $X$ .

Fig. 1 depicts the relation between mutual information and different entropies.

Fig. 1: Relation among entropy, joint entropy, conditional entropy and mutual information [MC12, Figure 6.5].

Quantum mutual information

Quantum mutual information is mutual information where the entropy is von Neumann entropy instead of Shannon entropy.

References

[MC12]

S. M. Moser and P.-N. Chen, A Student’s Guide to Coding and Information Theory, Cambridge University Press, 2012. Available at https://ebookcentral.proquest.com/lib/unisa/reader.action?docID=833494.

Keyword(s):

Cyber Engineering Knowledge Base

Math and physics (including quantum)

M

Mutual information

Classical mutual information

Quantum mutual information

References