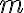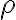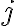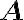Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
P |
|---|
Photon number splitting attack | ||||||
|---|---|---|---|---|---|---|
References
| ||||||
Positive operator-valued measure (POVM) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
The positive operator-valued measure (POVM) is a mathematical formalism/tool representing a measurement operation [NC10, Sec. 2.2.6; WN17, Sec. 1.5.1] that satisfies Postulate 3. Suppose a measurement described by measurement operators , where takes value from a finite set, is performed on a quantum system in the state , then the probability of outcome is given by Suppose we define then satisfies 1️⃣ the completeness relation and 2️⃣ is positive-semidefinite.
Example 1 [NC10, p. 92]
Suppose Alice gives Bob a qubit prepared in one of two states: Here is a measurement strategy for Bob to determine unequivocally whether he receives or . Define: Clearly satisfy the completeness relation, and by checking the definition of positive semidefiniteness, we can verify to be positive operators, so form a POVM. Let us now see how Bob can use to distinquish between and :
Using , Bob never mistakes for and vice versa, but Bob sometimes cannot determine which state he receives. Example 2 [WN17, Example 1.5.1]
Denote by an orthonormal basis. Define (a projector), and , then for each , where is a matrix with the basis vectors as columns. The linear independence of the basis vectors implies is nonsingular, and In other words, satisfies the completeness relation. When the POVM elements are projectors, such as in the preceding example, the POVM is called a projection-valued measure (PVM) [Hay17, p. 7]. Watch edX Lecture 1.6 “Generalized measurements” of Quantum Cryptography by CaltechDelftX QuCryptox. References
| ||||||||||||
Positive semidefiniteness and positive definiteness | ||||||
|---|---|---|---|---|---|---|
For Hermitian matrix , the following statements are equivalent, and any one can serve as the definition of the positive definiteness of [Mey00, Sec. 7.6; Woe16, Sec. 7.4]:
Similarly, the following statements are equivalent, and any one can serve as the definition of the positive semidefiniteness of : References
| ||||||
Projective measurement | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
The discussion here follows from the discussion of the positive operator-valued measure (POVM). The POVM cannot be used to determine the post-measurement state because the post-measurement state may not be pure [WN17, p. 13]. Instead, a Kraus operator representation of the POVM, known as projective measurement, is necessary to specify the post-measurement state. Projective measurements are repeatable, and the outcome observed as a result of projective measurement is deterministic [MM12, Sec. 2.7], as explained below.
Projective measurements are often discussed in terms of an observable, which is defined as a Hermitian operator acting on the state space of a system. Every observable has a spectral decomposition [Mey00, p. 517]: where are the eigenvalues of , and are so-called spectral/orthogonal projectors onto the null space of . More precisely, 1️⃣ are Hermitian and idempotent, 2️⃣ , and 3️⃣ are mutually orthogonal. Clearly, are valid POVM elements. A (non-unique) Kraus operator representation or Kraus decomposition of is defined as [WN17, Definition 1.5.2]:
With Kraus operators, we can now define projective measurement: Definition 1: Projective measurement [WN17, Definition 1.5.4; MM12, p. 153]
A projective measurement is given by a set of orthogonal projectors such that . By default, the Kraus operator is chosen to be . The probability of observing measurement outcome given initial state is The post-measurement state is
Since the default Kraus operators are the same as the orthogonal projectors, most authors skip discussion of Kraus operators altogether 🤷♂️. Measuring the observable is equivalent to performing a projective measurement with respect to the decomposition , where the measurement outcome corresponds to eigenvalue . Example 1 [KLM07, Example 3.4.1]
Consider the Pauli observable , i.e., the Pauli-Z operator/matrix: which does not change an input of , but flips to (which is equivalent to with a phase change). The Pauli-Z operator acts as a NOT operator in the Hadamard basis. has eigenpairs and , where the eigenvectors and are also called eigenstates [MM12, p. 338]. Thus, has spectral decomposition: with orthogonal projectors Interpreting the above, a projective measurement of is a measurement in the standard basis with eigenvalue corresponding to final state and eigenvalue corresponding to final state . Example 2 [WN17, Example 1.5.3]
Given a two-qubit state , suppose we want to measure the parity of the two qubits in the standard basis. One method is to measure in the (-dimensional) standard basis, obtain two classical bits, and take their parity. In this case, the probability of obtaining outcome “even” is and the post-measurement state is Another method is to measure the parity using projective measurement which directly projects onto the relevant subspaces, without measuring the qubits individually. Define projectors: which we can quickly verify to be orthogonal and conformant with the completeness relation: In this case, the probability of getting outcome “even” is which is the same as before; and the post-measurement state is The preceding two methods produce different outcomes on the EPR state , or in density-matrix representation, By measurement in the standard basis, the probability of getting outcome “even” is while the post-measurement state is By projective measurement, is the same as before, but the post-measurement state is different: Thus, projective measurement with does not change the EPR state. This is one of the main advantages of using projective measurement as opposed to basis measurement: the former enables simple computation (e.g., parity) on multi-qubit states without fully “destroying” the state, as basis measurement does. In Example 2, the observation that the projective measurement preserves the quantum state is not a coincidence. In fact, building on Definition 1, applying measurement to , i.e., applying to twice gives us [MM12, p. 153]: References
| ||||||||||||||||
Projector | ||||
|---|---|---|---|---|
A matrix is a projector if it is 1️⃣ Hermitian and 2️⃣ idempotent [Ber18, Definition 4.1.1]. References
| ||||
Pure state, mixed state, density operator/matrix | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
As defined in Practical 1 of COMP 5074, a qubit is a quantum state with two possible outcomes. Mathematically, a qubit is a two-dimensional Hilbert space. A pure state is the quantum state of a qubit that we can precisely define at any point in time [Qis21, Sec. 1].
In non-ideal conditions, a qubit can assume a certain quantum state at a certain probability, and other quantum states at other probabilities, regardless of measurements.
A direct but rather clunky representation of a mixed state is the set of pairs: where each pair means the pure state appears at probability , for . Note . A more compact and useful representation of a mixed state can be obtained from the type of Hilbert-space operators called density operators [KLM07, Sec. 3.5.1].
If the explanation above is hard to grasp, see if edX Lecture 1.2 “The density matrix” of Quantum Cryptography by CaltechDelftX QuCryptox helps. When applied with unitary operator , state evolves into . Accordingly, the density matrix of the mixed state evolves into Our adventure with the trace operator continues because an important application of the trace operator is determining the probability of getting result when applying measurement operator to mixed state . By definition, the probability of getting result given initial state is [NC10, p. 99]: The last equality is due to Eq. (1). By the law of total probability, Omitting the derivation in [NC10, pp. 99-100], the density matrix of the system after making measurement and obtaining result is: By the law of total probability, implying which is called the completeness equation. ⚠ Note is unitary if and only if has one value. Postulates of quantum mechanicsUsing the language of the density operator, we can phrase the fundamental postulates of quantum mechanics as [NC10, pp. 98-102; Gra21, p. 11-12]: Postulate 1: Associated with any isolated physical system is a complex-valued Hilbert space known as the state space of the system. The system is completely described by its density operator, which is a positive operator with trace one, acting on the state space of the system. If a quantum system is in the state (in density-matrix, not ket notation) with probability , then the density operator for the system is . Postulate 2: The evolution of a closed quantum system is described by a unitary transformation. That is, the state of the system at time is related to the state of the system at time by a unitary operator , which depends only on the times and : . Postulate 3 (aka Measurement Postulate): Quantum measurements are described by a collection of measurement operators. These are operators acting on the state space of the system being measured. The index refers to the measurement outcomes that may occur in the experiment. If the state of the quantum system is immediately before the measurement then the probability that result occurs is given by and the state of the system after the measurement is The measurement operators satisfy the completeness equation: Postulate 4: The state space of a composite physical system is the tensor product of the state spaces of the component physical systems. Moreover, if we have systems numbered 1 through , and system number is prepared in the state , then the joint state of the total system is . Postulate 3 defines general/generalised measurement [NC10, Box 2.5], which consists of 1️⃣ a rule describing the probabilities of different measurement outcomes, and 2️⃣ a rule describing the post-measurement state.
References
| ||||||||||||||