Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
S |
|---|
Schatten norm | ||||
|---|---|---|---|---|
For , suppose its singular values are . Then, the Schatten -norm of , where , is defined as [Ber09, Proposition 9.2.3]: When , we have the Schatten 1-norm, which is also called the trace norm or nuclear norm [Ber09, p. 549]: When , we have the Frobenius norm: References
| ||||
Schmidt decomposition | ||||
|---|---|---|---|---|
References
| ||||
Secret key rate | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
The secret key rate is the fraction of secure key bits produced per protocol round, where a round is the transmission of a quantum state through the quantum channel [Gra21, p. 38]. The secret key rate generally depends on the total number of rounds performed. The asymptotic secret key rate (often just asymptotic key rate) is the secret key rate when is assumed to simplify analysis.
Assuming is not realistic, and the security of a QKD protocol has to be analysed assuming a finite and generally finite resources. Analysis of the secret key rate and associated security properties of a QKD protocol is called finite-key analysis [TLGR12], to be covered in the future. References
| ||||||||||
Security of quantum key distribution (QKD): overview | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Methods for analysing the security of quantum key distribution (QKD) schemes/protocols are still being developed [PAB+20, PR22].
The security of a QKD scheme is typically analysed in terms of the level of success of 1️⃣ individual attacks, 2️⃣ collective attacks and 3️⃣ coherent attacks; in 🔼 increasing order of power given to the adversary [Wol21, Sec. 5.3.1].
The security of a QKD scheme is also often analysed in terms of composability, short for universally composable security.
TODO: Trace distance criterion [PR22], security = correctness + secrecy [Gra21]. Asymptotic vs finite-key security analysis. Security evaluation of practical QKD implementations involves evaluating the level of success of “quantum hacking” (i.e., side-channel attacks on QKD). References
| ||||||||||||||||||
Separable vs entangled | ||||
|---|---|---|---|---|
The joint state, , of two quantum systems and is separable [WN17, Definition 2.1.1] if there exists a probability distribution , and sets of density matrices and such that If such an expression for does not exist, is entangled [WN17, Definition 2.1.1]. Specifically, if is a pure state, then is separable if and only there exists and such that Example 1: [WN17, Example 2.1.3]
Example 2: [WN17, Example 2.1.2]
Example 3: [WN17, Example 2.1.1]
Example 4: [WN17, Example 2.1.4]
This example is meant to highlight the difference between the following two states: where . is separable whereas is not. Consider the outcomes of measuring subsystem in and in the standard basis and in the Hadamard basis. Measuring subsystem of in the Hadamard basis: Define the measurement operators to be and , where and . Clearly, and . Using projective measurement, the post-measurement state conditioned on measurement outcome is Let us work out the numerator and the denominator separately, starting with the numerator: The preceding equality follows from these identities, which you will derive in the practical: The denominator is: The preceding computation is tedious but straightforward given the right tool (e.g., NumPy). Combining the results for the numerator and denominator, we get Thus, upon measuring a on subsystem , subsystem can be in either or at equal probabilities; we say the reduced state on is maximally mixed. Measuring subsystem of in the Hadamard basis: The pair of and can be re-expressed as and , because ‘’ is orthogonal to ‘’ just as ‘’ is orthogonal to ‘’. The preceding statement implies when is measured on subsystem , subsystem is in state as well. References
| ||||
Singular value | ||||||
|---|---|---|---|---|---|---|
Singular values, like eigenvalues, are an intrinsic property of a matrix. Unsurprisingly, they can be defined in terms of eigenvalues: Definition 1: Singular value [Ber09, Definition 5.6.1]
Singular values can also be defined through the operation called singular value decomposition: Definition 2: Singular value decomposition and singular values [Hog13, Sec. 5.6]
References
| ||||||
Spectral theorem and spectral decomposition | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Spectral theorem is one of the fundamental theorems of linear algebra [ABH09, Sec. 3.6]. Based on the spectral theorem, spectral decomposition is an essential tool in quantum theory [NC10, Box 2.2]. Multiple equivalent interpretations of the spectral theorem exist, e.g., [ABH09, Theorems 3.6.4 and 3.6.12]. The interpretation in Theorem 1 directly defines spectral decomposition, and is hence also called the spectral decomposition theorem. Theorem 1: Spectral (decomposition) theorem [Hol13, Theorem 8.23; Zha11, Theorem 3.4; KLM07, Theorem 2.4.3]
Any normal operator, , has an outer product representation [KLM07, Sec. 2.4; Mey00, p. 517]: where The outer products are projectors that satisfy
References
| ||||||||||||||
SymPy | ||
|---|---|---|
SymPy is a Python library for symbolic computing. In symbolic computing, we reason with symbols rather than numeric values. When running SymPy in Google Colab, make sure you are using a WebKit-based browser such as Chrome or Edge. The first thing to do when using SymPy is creating symbols. There are seven ways to create a symbol. Right from the beginning, it is crucial to know how to make assumptions in SymPy.
| ||


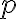
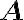
![p\in[1,\infty] p\in[1,\infty]](https://lo.unisa.edu.au/filter/tex/pix.php/d64227ec9eee9f2d1cb21f0459addc55.gif)
![\|\mathbf{A}\|_{\sigma p} \triangleq \begin{cases} \left[\sum_{i=1}^{\min(n,m)}\sigma_i^p(\mathbf{A}) \right]^{1/p}, & 1\leq p\lt\infty,\\ \sigma_\max(\mathbf{A}), & p = \infty.\end{cases} \|\mathbf{A}\|_{\sigma p} \triangleq \begin{cases} \left[\sum_{i=1}^{\min(n,m)}\sigma_i^p(\mathbf{A}) \right]^{1/p}, & 1\leq p\lt\infty,\\ \sigma_\max(\mathbf{A}), & p = \infty.\end{cases}](https://lo.unisa.edu.au/filter/tex/pix.php/9f539feeb7312ba8e6a9f8b7515eaf83.gif)
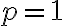


![\|\mathbf{A}\|_F \triangleq \left[\text{tr}(\mathbf{A}^\ast\mathbf{A})\right]^{1/2} = \|\mathbf{A}\|_{\sigma2}. \|\mathbf{A}\|_F \triangleq \left[\text{tr}(\mathbf{A}^\ast\mathbf{A})\right]^{1/2} = \|\mathbf{A}\|_{\sigma2}.](https://lo.unisa.edu.au/filter/tex/pix.php/862296e5fe62a65272394fdd0cb5c0e2.gif)


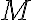


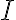
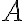
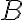
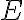






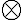




































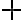

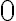
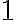









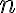














![(1, 1/\sqrt{2}[1 \; 1]^\top) (1, 1/\sqrt{2}[1 \; 1]^\top)](https://lo.unisa.edu.au/filter/tex/pix.php/3d5f032860eb51fb9bb5b31778fedd2e.gif)
![(-1, 1/\sqrt{2}[-1 \; 1]^\top) (-1, 1/\sqrt{2}[-1 \; 1]^\top)](https://lo.unisa.edu.au/filter/tex/pix.php/302a8b3e6ef008ebe240fe4692b4d52f.gif)
