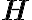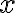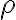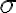Browse the glossary using this index

Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL

T

Time evolution of quantum systems

by Yee Wei Law - Tuesday, 29 August 2023, 9:50 AM

At the highest level, the time-evolution postulate of quantum theory [KLM07, p. 44] states

The time-evolution of the state of a closed quantum system is described by a unitary operator. That is, for any evolution of the closed system, there exists a unitary operator

$\mathbf{U}$ such that if the initial state of the system is

$|\psi\rangle$ , then after the evolution, the state of the system will be

$\mathbf{U}|\psi\rangle$ .

But how do we arrive at the understanding of the role of the unitary operator?

Consider the evolution of one quantum state:

$\alpha_1|x_1\rangle + \cdots + \alpha_n|x_n\rangle$

to another quantum state:

$\alpha'_1|x_1\rangle + \cdots + \alpha'_n|x_n\rangle,$

where $|x_1\rangle, \ldots, |x_n\rangle$ are basis state vectors. Suppose there exists a linear operator $\mathbf{U}$ that captures this evolution:

$\begin{bmatrix}\alpha'_1 \\ \vdots \\ \alpha'_n\end{bmatrix} = \mathbf{U}\begin{bmatrix}\alpha_1 \\ \vdots \\ \alpha_n\end{bmatrix},$

such that $\sum_{i=1}^n|\alpha'_i|^2 = \sum_{i=1}^n|\alpha_i|^2$ . Besides linearity and conservation of overlaps (overlap of a vector with itself = norm squared), there are other properties that $\mathbf{U}$ must satisfy.

Define $\mathbf{U}(t)$ as a time-dependent map of one quantum state to another: $|\psi(t)\rangle = \mathbf{U}(t)|\psi(0)\rangle$ , then the additional properties that $\mathbf{U}(t)$ must satisfy are [Hir04, Sec. 8.3.1]:

Decomposability: $\mathbf{U}(t_1+t_2) = \mathbf{U}(t_1)\mathbf{U}(t_2), \forall t_1,t_2\in\mathbb{R}$ .
Continuity/smoothness: $|\psi(t')\rangle = \lim_{t\to t'}|\psi(t)\rangle = \lim_{t\to t'}\mathbf{U}(t)|\psi(0)\rangle$ .

To satisfy 1️⃣ linearity, 2️⃣ conservation of overlaps and 3️⃣ decomposability, $\mathbf{U}(t)$ must be unitary; see proof in [Hir04, Lemma 8.3.1].

Think of a unitary operator as a matrix transformation using a unitary matrix. A unitary matrix is a matrix whose Hermitian conjugate / Hermitian adjoint / conjugate transpose is also its inverse:

$\begin{align} \mathbf{U}^\dagger = \mathbf{U}^{-1} \implies \mathbf{UU}^\dagger = \mathbf{U}^\dagger\mathbf{U} = \mathbb{1}, \end{align}$

where $\mathbb{1}$ is the identity matrix of the appropriate dimensions.

About the notation, many quantum physicists prefer to use 1️⃣ $^\dagger$ instead of $^\ast$ to denote Hermitian conjugate, and 2️⃣ $\mathbb{1}$ instead of $\mathbf{I}$ to denote the identity matrix.

The unitarity of quantum evolution implies reversibility since $|\psi(t)\rangle = \mathbf{U}(t)|\psi(0)\rangle$ $\implies|\psi(0)\rangle = \mathbf{U}^\dagger(t)|\psi(t)\rangle$ .

Unlike classical logic gates, quantum gates are governed by unitary matrices and are thus reversible.

However, measurements are not reversible; this is known as the measurement paradox of quantum physics [Hir04, p. 23].

A unitary operator is a normal operator because it commutes with its Hermitian conjugate, i.e., $\mathbf{UU}^\dagger = \mathbf{U}^\dagger\mathbf{U}$ [KLM07, Definition 2.4.1]. 👈 This property enables the spectral decomposition of a unitary operator.

To additionally satisfy continuity, Stone’s theorem [Par92, Sec. I.13] necessitates the existence of a Hermitian / self-adjoint operator $\mathbf{H}$ such that

$\mathbf{U}(t) = e^{-i\mathbf{H}t}, \tag{1}$

where $\mathbf{H}$ is called the (quantum) Hamiltonian or Hamilton operator representing the total energy of the closed quantum system [Hir04, Theorem 8.3.1].

The exponential in Eq. (1) is a matrix exponential:

$e^{\mathbf{X}} \triangleq \sum_{n=0}^\infty \frac{1}{n!}\mathbf{X}^n.$

More info about the matrix exponential is available in the knowledge base entry on state-space equations.

Sometimes, Eq. (1) is written as $\mathbf{U}(t) = e^{-i\mathbf{H}t/\hbar}$ , where $\hbar$ is the Planck’s constant whose value must be experimentally determined [NC10, p. 82].

Thus, $|\psi(t)\rangle = e^{-i\mathbf{H}t}|\psi(0)\rangle$ , implying

$|\dot{\psi}(t)\rangle = -i\mathbf{H}e^{-i\mathbf{H}t}|\psi(0)\rangle = -i\mathbf{H}|\psi(t)\rangle,$

which is usually written in the following form:

$i|\dot{\psi}(t)\rangle = \mathbf{H}|\psi(t)\rangle.$

The linear differential equation above is called the general version of the time-dependent Schrödinger equation [Wei15, p. 82], which is sometimes called the abstract Schrödinger equation [Hir04, p. 131].

Summarising the discussion so far, the time-evolution postulate can be rephrased in more precise mathematical terms [NC10, Postulate 2']:

The time evolution of the state of a closed quantum system is described by the Schrödinger equation:

$i|\dot{\psi}(t)\rangle = \mathbf{H}|\psi(t)\rangle.$

References

[Hir04]	M. Hirvensalo, Quantum Computing, 2nd ed., Natural Computing Series, Springer Berlin, Heidelberg, 2004. https://doi.org/10.1007/978-3-662-09636-9.
[KLM07]	P. Kaye, R. Laflamme, and M. Mosca, An Introduction to Quantum Computing, Oxford University Press, 2007. Available at https://ebookcentral.proquest.com/lib/unisa/reader.action?docID=415080.
[NC10]	M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information, 10th anniversary ed., Cambridge University Press, 2010. Available at http://mmrc.amss.cas.cn/tlb/201702/W020170224608149940643.pdf.
[Par92]	K. Parthasarathy, An Introduction to Quantum Stochastic Calculus, Birkhäuser Basel, 1992. https://doi.org/10.1007/978-3-0348-0566-7.
[SF15]	L. Susskind and A. Friedman, Quantum Mechanics: The Theoretical Minimum, Penguin Press, 2015.
[Wei15]	S. Weinberg, Lectures on Quantum Mechanics, 2nd ed., Cambridge University Press, 2015. https://doi.org/10.1017/CBO9781316276105.

Trace distance

by Yee Wei Law - Saturday, 2 September 2023, 7:44 PM

Measurement of information is crucial to cybersecurity. One of these measures is distance measure between two quantum states.

Static measures quantify how close two quantum states are [NC10, p. 399].
Dynamic measures quantify how well information is preserved during a dynamic process [NC10, p. 399]. Dynamic measures can be derived from static measures.

Distance measures are defined in a way that makes sense to the analysis they are applied to, hence more than one distance measure exist in the literature, but two of these measures are in particularly wide use, namely trace distance and fidelity.

The focus here is trace distance, which for probability density functions $p_x,q_x$ and index set $x$ is defined to be [NC10, Eq. (9.1)]:

$D(p_x, q_x) \triangleq \frac{1}{2}\sum_x |p_x - q_x|.$

Trace distance is also called $L_1$ distance and Kolmogorov distance.

Trace distance satisfies the mathematical definition of metric, because it satisfies [NC10, p. 400]:

Symmetry, i.e., $D(p_x,q_x)=D(q_x,p_x)$ .
Non-negativity, i.e., $D(p_x,q_x)\begin{cases}>0&\text{if }p_x \neq q_x,\\=0&\text{otherwise.}\end{cases}$
Triangle inequality, i.e., $D(p_x,r_x) \leq D(p_x,q_x) + D(q_x,r_x)$ .

Extending the earlier definition to quantum states, the trace distance between density matrices $\rho$ and $\sigma$ is defined as [MM12, Sec. 3.11]:

$D(\rho,\sigma)\triangleq\frac{1}{2}\text{tr}|\rho-\sigma|.$

References

[Cho22]	M.-S. Choi, A Quantum Computation Workbook, Springer Cham, 2022. https://doi.org/10.1007/978-3-030-91214-7.
[MM12]	D. C. Marinescu and G. M. Marinescu, Classical and Quantum Information, Elsevier, 2012. https://doi.org/10.1016/C2009-0-64195-7.
[NC10]	M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information, 10th anniversary ed., Cambridge University Press, 2010. Available at http://mmrc.amss.cas.cn/tlb/201702/W020170224608149940643.pdf.

Keyword(s):

Trace norm

by Yee Wei Law - Saturday, 11 March 2023, 3:17 PM

The trace norm is an example of a unitarily invariant norm and is equivalent to the Schatten 1-norm.

References

[Ber09]	D. R. Bernstein, Matrix Mathematics: Theory, Facts, and Formulas, 2nd ed., Princeton University Press, 2009.
[Hog13]	L. Hogben (ed.), Handbook of Linear Algebra, 2nd ed., CRC Press, 2013. https://doi.org/10.1201/b16113.

Keyword(s):

Trace operator

by Yee Wei Law - Tuesday, 14 March 2023, 5:34 PM

The trace of a square matrix $\mathbf{A}$ , denoted by tr $\mathbf{A}$ or tr $(\mathbf{A})$ , is a linear map that maps the matrix to a complex number, and is specifically the sum of the diagonal elements of the matrix.

Obvious properties:

$\text{tr}\mathbf{A} = \text{tr}\mathbf{A}^\top$ [Ber18, p. 287].
If $\mathbf{AB}$ and $\mathbf{BA}$ are square matrices, then the cyclic property applies: $\text{tr}(\mathbf{AB}) = \text{tr}(\mathbf{BA})$ [Ber18, p. 287].

Useful property involving brakets:

If $\mathbf{A}$ is an $n\times n$ matrix, then $\text{tr}(\mathbf{A}) = \sum_i\langle i | \mathbf{A}| i\rangle$ , where $\{|i\rangle\}$ is any orthonormal basis of $\mathbb{C}^n$ [WN17, Definition 1.2.4].

References

[Ber18]	D. S. Bernstein, Scalar, Vector, and Matrix Mathematics: Theory, Facts, and Formulas - Revised and Expanded Edition, Princeton University Press, 2018. https://doi.org/10.1515/9781400888252.
[WN17]	S. Wehner and N. Ng, Lecture Notes: edX Quantum Cryptography, 2017. Available at https://courses.edx.org/courses/course-v1:CaltechDelftX+QuCryptox+ 3T2018/pdfbook/0/.

Keyword(s):

Cyber Engineering Knowledge Base

Math and physics (including quantum)

T

Time evolution of quantum systems

References

Trace distance

References

Trace norm

References

Trace operator

References