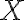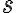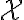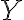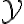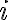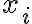Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
M |
|---|
Mutual information | ||||
|---|---|---|---|---|
The following introduces classical mutual information before quantum mutual information. Classical mutual informationConsider the channel model of a transmission system in Fig. 1. Since the input takes a certain value at a certain probability, the input is a discrete random variable, which we denote by .
Suppose the sender transmits the th input symbol as at a probability of , this probability is called the prior probability of . “Prior probability” is often written in Latin as “a priori probability”. Suppose the receiver receives as the th output symbol, the probability of this output conditioned on the th input being is the likelihood of : . However in most cases, we are more interested in the posterior probability of : , i.e., what is the probability that the th input is given the th output is . “Posterior probability” is often written in Latin as “a posteriori probability”. The posterior probability helps us determine the amount of information that can be inferred about the input when the output takes a certain value. The information gain or uncertainty loss about input upon receiving output is the mutual information of and , denoted by [MC12, pp. 126-127].
Extending the result above from to and from to , we define the system/average mutual information of and , denoted by , as the information gain or uncertainty loss about random variable by observing random variable [MC12, Definition 6.7]: It is trivial to show that 1️⃣ , 2️⃣ , 3️⃣ iff and are independent. Omitting the derivation in [MC12, p. 129], where denotes the Shannon entropy of . Fig. 1 depicts the relation between mutual information and different entropies. Quantum mutual informationQuantum mutual information is mutual information where the entropy is von Neumann entropy instead of Shannon entropy. References
| ||||