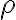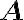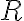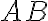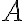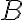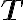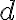Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
A |
|---|
Abstract algebra | |||
|---|---|---|---|
See 👇 attachment or the latest source on Overleaf, on the topics of groups and Galois fields (pending). | |||
Ancilla | ||||||
|---|---|---|---|---|---|---|
An ancilla (system) is an auxiliary quantum-mechanical system [ETS18]. Think of ancilla as something extra that is used to achieve some goal [Pre18]. References
| ||||||
Axiomatic approach to quantum operations | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
In quantum information theory, the foundation of quantum cryptography, the concepts of general/generalised measurements and quantum channels are rooted in the concept of quantum operation [Pre18, Sec. 3.2.4].
While the time evolution of a closed quantum system can be expressed using a single unitary operator, the time evolution of an open quantum system is much less straightforward [HXK20], and this is where the theory of quantum operations come in. Here, the axiomatic approach in [NC10, Sec. 8.2.4] to defining quantum operations is discussed, starting with Definition 1. Definition 1: Quantum operation [NC10, p. 367]
A quantum operation is a map from the set of density operators for the input space to the set of density operators for the output space , that satisfies these axioms:
Justification of Axiom 1: In the absence of measurement, by itself completely describes the quantum operation, and Axiom 1 reduces to the requirement that ; in this case, the quantum operation is trace-preserving.
Justification of Axiom 2: Let , then where is a normalisation factor. By Bayes’ rule, Justification of Axiom 3: A quantum operation maps a density operator to a density operator — by itself or as part of a larger system — and density operators are always positive, so must be a completely positive map. Example 1 [Pre18, p. 19]
This example is meant to show that the transpose operation is not a completely positive map and hence not a quantum operation. We first observe that is positive if is positive because the quadratic form However, the transpose operation is not completely positive due to the following. Suppose system contains entangled subsystems and , and has state , ignoring the normalisation constant. Above, we applied the identity . Now consider the composite map , where is the transpose operation, which transforms to . Applying the composite map to , we get Applying the composite map to the above, we get back Therefore, if we represent the map with a square matrix, the matrix is involutory (square = identity), and it is trivial to show that the eigenvalues of an involutory matrix are (see below), implying the composite map is not positive. In other words, the transpose operation is not a completely positive map, and hence not a quantum operation. Axioms 1-3 lead to the following important theorem. Theorem 1 [NC10, Theorem 8.1]
In Theorem 1,
Example 2 [MM12, p. 176]
The freedom in the operator-sum representation is especially useful for studying quantum error correction. Theorem 2 [NC10, Theorem 8.3]
Watch lectures on Kraus representations by Artur Ekert, inventor of the E91 QKD protocol: References
| ||||||||||||||||||