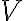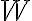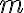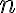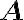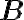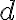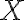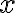Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
C |
|---|
Coherent attack | |||
|---|---|---|---|
The discussion here follows from the discussion of collective attacks. | |||
Coherent state | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
A coherent state is a special quantum state that a coherent laser ideally emits [Wil07, p. 19]. That 👆 does not say much, but there is no straightforward way to define “coherent state”, a concept introduced by Schrödinger [SZ97, p. 46]. Mathematically and in short, a coherent state is the eigenstate of the positive frequency part of the electric field operator [SZ97, p. 46], but this requires definition of the electric field operator, which in turn requires discussion of the quantization of electromagnetic fields. Classically, an electromagnetic field consists of waves with well-defined amplitude and phase, but in quantum mechanics, this is no longer true. More precisely, there are fluctuations in both the amplitude and phase of the field [SZ97, Ch. 2]. A coherent state is a state that has the same fluctuations of quadrature amplitudes as the vacuum state but which possibly has nonzero average quadrature amplitudes [Van06, Sec. 4.6.1]. References
| ||||||||||
Collective attack | ||||||||
|---|---|---|---|---|---|---|---|---|
The discussion here follows from the discussion of individual attacks. In a collective attack [Sch10],
References
| ||||||||
Composite quantum systems | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Consider a multi-qubit system consisting of two qubits. There are four possible final states: ; and it makes sense to express the quantum state of this two-qubit system as the linear combination: where the normalisation rule still applies: An alternative representation of is where the subscript indicates the order of the system. Some authors call the set , and equivalently , the tensor base [Des09, p. 316]. Watch Microsoft Research’s presentation on “Quantum Computing for Computer Scientists”: In the vector representation, given two separated qubits: their collective state can be expressed using the Kronecker product (also called the matrix direct product and tensor product): Multiple shorthands exist for : 1️⃣ , 2️⃣ , 3️⃣ [Mer07, p. 6; NC10, Sec. 2.1.7]; we have used the third shorthand earlier. In general, we can compose the Hilbert space of a multi-qubit system using the vector space direct product (also called tensor direct product) of lower-dimensional Hilbert spaces [NC10, Sec. 2.1.7]:
Classical-quantum stateIn quantum cryptography, we often encounter states that are partially classical and partially quantum. A classical state (c-state for short) is a state defined by a density matrix that is diagonal in the standard basis of the -dimensional state space of , i.e., has the form: Suppose we prepare the following states for Alice and Bob: with probability 1/2, we prepare and with probability 1/2, we prepare . Then, the joint state is the so-called classical-quantum state (cq-state for short): In quantum-cryptographic convention,
Formally,
References
| ||||||||||||